ITA 2018 - 1º Dia - Física - Questões com Gabarito e Resolução* Quando precisar use os seguintes valores para as constantes: Constante ...
ITA 2018 - 1º Dia - Física - Questões com Gabarito e Resolução*
Quando precisar use os seguintes valores para as constantes:
Constante da gravitação universal G = 7×10⁻¹¹ m³/kg.s². Aceleracão da gravidade g = 10 m/s². Velocidade do som no ar = 340 m/s. Raio da Terra R = 6 400 km. Constante dos gases R = 8,3J/mol.K. Índice adiabático do ar γ = CP/CV = 1,4. Massa molecular do ar Mar = 0,029 kg/mol. Permeabilidade magnética do vácuo µ0 = 4π × 10⁻⁷ N/A². Pressão atmosférica 1,0atm = 100 kPa. Massa específica da água = 1,0 g/cm3³.
VAMOS ÀS QUESTÕES DE FÍSICA.
01. Considere uma estrela de nêutrons com densidade média de 5 × 10¹⁴ g/cm³, sendo que sua frequência de vibração radial ν é função do seu raio R, de sua massa m e da constante da gravitação universal G. Sabe-se que ν é dada por uma expressão monomial, em que a constante adimensional de proporcionalidade vale aproximadamente 1. Então o valor de ν é da ordem de
A ( ) 10⁻² Hz.
B ( ) 10⁻¹ Hz.
C ( ) 10⁻⁰ Hz.
D ( ) 10² Hz.
E ( ) 10⁴ Hz.
Desprezando o atrito, pode-se dizer que, com 12 m/s de velocidade inicial, a bola
a) bate na rede.
b) passa tangenciando a rede.
c) passa a rede e cai antes da linha de fundo.
d) passa a rede e cai na linha de fundo.
e) passa B rede e cai fora da quadra.
Resposta.
03. Sobre uma prancha horizontal de massa desprezível e apoiada no centro, dois discos, de massas mA e mB, respectivamente, rolam com as respectivas velocidades vA e vB, constantes, em direção ao centro, do qual distam LA e LB, conforme a figura.
Com o sistema em equilíbrio antes que os discos colidam, a razão vA/vB é dada por
A ( ) 1.
B ( ) mA/mB.
C ( ) mB/mA.
D ( ) LAmA/LBmB.
E ( ) LBmB/LAmA.
Resposta.
04. Uma haste vertical de comprimento L, sem peso, é presa a uma articulação T e dispõe em sua extremidade de uma pequena massa m que, conforme a figura, toca levemente a quina de um bloco de massa M. Após uma pequena perturbação, o sistema movimenta-se para a direita. A massa m perde o contato com M no momento em que a haste perfaz um ângulo de π/6 rad com a horizontal.
Desconsiderando atritos, assinale a velocidade final do bloco.
Resposta.
05. Em queixa à polícia, um músico depõe ter sido quase atropelado por um carro, tendo distinguido o som em Mi da buzina na aproximação do carro e em Ré, no seu afastamento. Então, com base no fato de ser de 10/9 a relação das frequências vMi/vRé, a perícia técnica conclui que a velocidade do carro, em km/h, deve ter sido aproximadamente de
A ( ) 64.
B ( ) 71.
C ( ) 83.
D ( ) 102.
E ( ) 1307.
Resposta.
06. Na figura, o tanque em forma de tronco de cone, com 10,0cm de raio da base, contém água até o nível de altura h = 500cm, com 100 cm de raio da superfície livre.
Removendo-se a tampa da base, a água começa a escoar e, nesse instante, a pressão no nível a 15,0cm de altura é de
A ( ) 100 kPa.
B ( ) 102 kPa.
C ( ) 129 kPa.
D ( ) 149 kPa.
E ( ) 150 kPa.
Resposta.
07. A partir de um mesmo ponto a uma certa altura do solo, uma partícula é lançada sequencialmente em três condições diferentes, mas sempre com a mesma velocidade inicial horizontal v0. O primeiro lançamento é feito no vácuo e o segundo, na atmosfera com ar em repouso. O terceiro é feito na atmosfera com ar em movimento cuja velocidade em relação ao solo é igual em módulo, direção e sentido à velocidade v0. Para os três lançamentos, designando-se respectivamente de t1, t2 e t3 os tempos de queda da partícula e de v1, v2 e v3 os módulos de suas respectivas velocidades ao atingir o solo, assinale a alternativa correta.
a) t1 < t3 < t2; v1 > v3 > v2
b) t1 < t2 = t3; v1 > v3 > v2
c) t1 = t3 < t2; v1 = v3 > v2
d) t1 < t2 < t3; v1 = v3 > v2
e) t1 < t2 = t3; v1 > v2 = v3
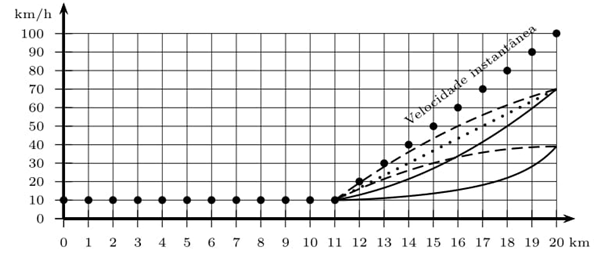
a) a tracejada que termina acima de 50 km/h.
b) a cheia que termina acima de 50 km/h.
c) a tracejada que termina abaixo de 50 km/h.
d) a pontilhada.
e) a cheia que termina abaixo de 50 km/h.
Resposta.
09. Uma massa m de carga q gira em órbita circular de raio R e período T no plano equatorial de um ímã. Nesse plano, a uma distância r do ímã, a intensidade do campo magnético é B(r) = µ/r³, em que µ é uma constante. Se fosse de
a) T/2.
b) 2T.
c) 8T.
d) 32T.
e) 64T.
Então, quando na posição mais baixa, o corpo terá uma velocidade relativa ao tubo, em cm/s, igual a
a) –11,3.
b) –206.
c) 11,3.
d) 206.
e) 194.
Resposta.
11. Num plano horizontal liso, presas cada qual a uma corda de massa desprezível, as massas ml e m2 giram em órbitas circulares de mesma frequência angular uniforme, respectivamente com raios r1 e r2 = r1/2. Em certo instante essas massas colidem-se frontal e elasticamente e cada qual volta a perfazer um movimento circular uniforme. Sendo iguais os módulos das velocidades de m1 e m2 após o choque, assinale a relação m2/ml.
a) 1
b) 3/2
c) 4/3
d) 5/4
e) 7/5
Considerando que ambos os sistemas estão separados por uma distância r muito maior que a1 e a2, conforme a figura, e que (1 + z)⁻² ≃ 1 − 2z + 3z² para z ≪ 1,, a força exercida pelo sistema 1 sobre o sistema 2 é
Resposta.
13. Quatro corpos pontuais, cada qual de massa m, atraem-se mutuamente devido à interação gravitacional. Tais corpos encontram-se nos vértices de um quadrado de lado L girando em torno do seu centro com velocidade angular constante. Sendo G a constante de gravitação universal, o período dessa rotação é dado por
Resposta.
14. Dois espelhos esféricos interdistantes de 50 cm, um côncavo, E1, e outro convexo, E2, são dispostos coaxialmente tendo a mesma distância focal de 16 cm. Uma vela é colocada diante dos espelhos perpendicularmente ao eixo principal, de modo que suas primeiras imagens conjugadas por E1 e E2 tenham o mesmo tamanho. Assinale a opção com as respectivas distâncias, em cm, da vela aos espelhos E1 e E2.
a) 25 e 25
b) 41 e 9
c) 34 e 16
d) 35 e 15
e) 40 e 10
a) Aumenta-se a intensidade do feixe de raio X e diminui-se a velocidade dos elétrons.
b) Aumenta-se a frequência dos raios X e triplica-se o número de elétrons no feixe.
c) Aumentam-se o comprimento de onda dos raios X e a energia cinética dos elétrons.
d) Dobram-se a distância entre camadas d (pela escolha de outro material) e o comprimento de onda dos raios X. Além disso, diminui-se a velocidade dos elétrons pela metade.
e) Diminui-se a intensidade dos raios X e aumenta-se a energia dos elétrons.
Resposta.
16. Três molas idênticas, de massas desprezíveis e comprimentos naturais l, são dispostas verticalmente entre o solo e o teto a 3l, de altura. Conforme a figura, entre tais molas são fixadas duas massas pontuais iguais.
Na situação inicial de equilíbrio, retira-se a mola inferior (ligada ao solo) resultando no deslocamento da massa superior de uma distância d1 para baixo, e da inferior, de uma distância d2 também para baixo, alcançando-se nova posição de equilíbrio. Assinale a razão d2/d1.
a) 2
b) 3/2
c) 5/3
d) 4/3
e) 5/4
Resposta.
17. No livro Teoria do Calor (1871), Maxwell, escreveu referindo-se a um recipiente cheio de ar:
“... iniciando com uma temperatura uniforme,
vamos supor que um recipiente é dividido em
duas partes por uma divisória na qual existe um
pequeno orifício, e que um ser que pode ver as moléculas
individualmente abre e fecha esse orifício
de tal modo que permite somente a passagem de
moléculas rápidas de A para B e somente as lentas
de B para A. Assim, sem realização de trabalho,
ele aumentará a temperatura de B e diminuirá a
temperatura de A em contradição com ... ”
Assinale a opção que melhor completa o texto de Maxwell.
a) a primeira lei da termodinâmica.
b) a segunda lei da termodinâmica.
c) a lei zero da termodinâmica.
d) o teorema da energia cinética.
17. No livro Teoria do Calor (1871), Maxwell, escreveu referindo-se a um recipiente cheio de ar:
“... iniciando com uma temperatura uniforme,
vamos supor que um recipiente é dividido em
duas partes por uma divisória na qual existe um
pequeno orifício, e que um ser que pode ver as moléculas
individualmente abre e fecha esse orifício
de tal modo que permite somente a passagem de
moléculas rápidas de A para B e somente as lentas
de B para A. Assim, sem realização de trabalho,
ele aumentará a temperatura de B e diminuirá a
temperatura de A em contradição com ... ”
Assinale a opção que melhor completa o texto de Maxwell.
a) a primeira lei da termodinâmica.
b) a segunda lei da termodinâmica.
c) a lei zero da termodinâmica.
d) o teorema da energia cinética.
Resposta.
19. Um pêndulo simples de massa m e haste rígida de comprimento h é articulado em torno de um ponto e solto de uma posição vertical, conforme a Figura 1. Devido à gravidade, o pêndulo gira atingindo uma membrana ligada a um tubo aberto em uma das extremidades, de comprimento L e área da seção transversal S (Figura 2). Após a colisão de reduzida duração, ∆t, o pêndulo recua atingindo um ângulo máximo θ (Figura 3). Sejam ρ a densidade de equilíbrio do ar e c a velocidade do som. Supondo que energia tenha sido transferida somente para a harmônica fundamental da onda sonora plana no tubo, assinale a opção com a amplitude da oscilação das partículas do ar.
Resposta.
20. Dois recipientes A e B de respectivos volumes VA e VB = βVA, constantes, contêm um gás ideal e são conectados por um tubo fino com válvula que regula a passagem do gás, conforme a figura.
Inicialmente o gás em A está na temperatura TA sob pressão PA e em B, na temperatura TB sob pressão PB. A válvula é então aberta até que as pressões finais PAf e PBf alcancem a proporção PAf /PBf = α, mantendo as temperaturas nos seus valores iniciais. Assinale a opção com a expressão de PAf.
As questões dissertativas, numeradas de 21 a 30, devem ser desenvolvidas, justificadas e respondidas no caderno de soluções.
21. Uma prancha homogênea de massa m é sustentada por dois roletes, interdistantes de 2l, que giram rapidamente em sentidos opostos, conforme a figura. Inicialmente o centro de massa da prancha dista x da linha intermediária entre os roletes. Sendo µ o coeficiente de atrito cinético entre os roletes e a prancha, determine a posição do centro de massa da prancha em função do tempo.
Resposta.
22. Uma esfera sólida e homogênea de volume V e massa específica ρ repousa totalmente imersa na interface entre dois líquidos imiscíveis. O líquido de cima tem massa específica ρc e o de baixo, ρb, tal que ρc < ρ < ρb· Determine a fração imersa no líquido superior do volume da esfera.
23. Dois capacitores em paralelo de igual capacitância C estão ligados a uma fonte cuja diferença de potencial é U. A seguir, com essa fonte desligada, introduz-se um dielétrico de constante dielétrica k num dos capacitores, ocupando todo o espaço entre suas placas. Calcule:
a) a carga livre que flui de um capacitor para outro;
b) a nova diferença de potencial entre as placas dos capacitores;
c) a variação da energia total dos capacitores entre as duas situações.
Resposta.
24. Seja um cometa numa órbita elíptica com as distâncias do afélio, ra, e periélio, rp. Com o Sol num dos focos como origem de um sistema de coordenadas polares, a equação que descreve o módulo do vetor posição r em função do ângulo θ medido a partir do periélio é r(θ) = α/(1 + ε cos θ), em que α e ε são constantes, sendo 0 < ε < 1. Expresse a excentricidade ε, a constante α e o período da órbita em função de ra e rp.
Resposta.
25. Na figura, os dois trens se aproximam, um com velocidade constante v1 = 108 km/h e o outro com velocidade também constante v2 = 144 km/h. Considere os trens condutores perfeitos e os trilhos interdistantes de d = 2,0 m, com resistência elétrica por unidade de comprimento igual a 0,10 Ω/km.a) a carga livre que flui de um capacitor para outro;
b) a nova diferença de potencial entre as placas dos capacitores;
c) a variação da energia total dos capacitores entre as duas situações.
Resposta.
24. Seja um cometa numa órbita elíptica com as distâncias do afélio, ra, e periélio, rp. Com o Sol num dos focos como origem de um sistema de coordenadas polares, a equação que descreve o módulo do vetor posição r em função do ângulo θ medido a partir do periélio é r(θ) = α/(1 + ε cos θ), em que α e ε são constantes, sendo 0 < ε < 1. Expresse a excentricidade ε, a constante α e o período da órbita em função de ra e rp.
Resposta.
Sabendo que em t = 0 os trens estão a 10 km de distância entre si e que o componente vertical local do campo magnético da Terra é B = 5,0 × 10−5 T, determine a corrente nos trilhos em função do tempo.
Resposta.
26. Contando com um prisma e um contador de número de fótons por segundo, deseja-se medir a temperatura de uma estrela com base no seu espectro eletromagnético obtido por meio de um telescópio.
a) Projete esquematicamente esse experimento representando o prisma como um triângulo e o contador de fótons por segundo como um quadrado.
b) Explique os conceitos usados em (a) para obter a temperatura da estrela.
27. No circuito abaixo os medidores de corrente e de tensão elétrica possuem resistência interna. Sabendo-se que a fonte fornece a ddp U, o voltímetro mede 4,0 V, o amperímetro mede 1,0 A e que os valores das resistências R1, R2 e R3 estão indicadas na figura, calcule o valor da resistência interna do voltímetro.
Resposta.
28. Na figura, presa a um fio de comprimento de 1,0 m, uma massa de 1,0 kg gira com uma certa velocidade angular num plano vertical sob a ação da gravidade, com eixo de rotação a h = 6,0 m do piso. Determine a velocidade angular mínima dessa massa para a ruptura do fio que suporta no máximo a tração de 46 N, bem como a distância ao ponto P do ponto em que, nesse caso, a massa tocará o solo.Resposta.
Determine a energia potencial do elétron no estado final desse átomo, sabendo que energia total no estado n é En = –13,6/n² eV e o raio é r = n² rB , em que rB é o raio de Bohr e n = 1, 2, 3 ⋅⋅⋅.
Resposta.
30. A figura mostra um fio por onde passa uma corrente I conectado a uma espira circular de raio a. A semicircunferência superior tem resistência igual a 2R e a inferior, igual a R. Encontre a expressão para o campo magnético no centro da espira em termos da corrente I.
Resposta.
*resolução Objetivo e ETAPA.





























COMENTÁRIOS