Prova de Estatística ENADE 2009 com Gabarito
Prova de Estatística ENADE 2009 com Gabarito
CONHECIMENTO ESPECÍFICO
ENADE 2009 - QUESTÃO 11
Com base no histórico de vendas de um certo produto, o Estatístico de uma empresa determinou que a comercialização desse item contribuirá para o lucro da empresa com um ganho de 30 mil reais, com probabilidade de 0,3; com um ganho de 8 mil reais, com probabilidade 0,5; e com uma perda de 5 mil reais, com probabilidade 0,2.
O lucro esperado da empresa com esse produto é
A) 10 mil reais.
B) 11 mil reais.
C) 12 mil reais.
D) 18 mil reais.
E) 14 mil reais.
ENADE 2009 - QUESTÃO 12
Um laboratório está avaliando a compra de uma estufa de certa marca, que possui temperatura média de operação igual a 200 graus Fahrenheit, com desvio-padrão de 10 graus Fahrenheit. Para elaborar um manual de operação, a temperatura deve ser medida em graus Celsius. Usando a expressão simplificada C = 0,6 F - 18 para converter graus Fahrenheit em graus Celsius, o Estatístico responsável encontrou que a média e o desvio-padrão da temperatura de operação da estufa são, respectivamente:
A) 102 graus Celsius e 6 graus Celsius.
B) 102 graus Celsius e 36 graus Celsius.
C) 120 graus Celsius e 6 graus Celsius.
D) 120 graus Celsius e 36 graus Celsius.
E) 182 graus Celsius e 6 graus Celsius.
ENADE 2009 - QUESTÃO 13
Sejam Y o número de pessoas que está na fila de uma Agência dos Correios em um dado minuto, e X o número de pessoas na fila que irá postar uma encomenda expressa. A distribuição conjunta de X e Y é dada na tabela:
Em certo minuto, dado que há seis clientes na fila, a probabilidade de que quatro deles postem uma encomenda expressa é
A) 0,006.
B) 0,028.
C) 0,140.
D) 0,192.
E) 0,200.
ENADE 2009 - QUESTÃO 15
O dono de uma lan house (loja que aluga computadores para acesso à internet) quer saber se o tempo de uso da internet por sessão é diferente entre seus clientes jovens e adultos.
Para isso, ele contratou um Estatístico, que coletou uma amostra aleatória de clientes nos dois grupos e mediu o tempo, em minutos, que cada cliente gastou em sua sessão.
Os dados coletados estão resumidos nas duas ogivas (dois polígonos de frequências acumuladas) mostradas na figura:
Com base no gráfico, o Estatístico pode concluir que
A) cerca de 80% por cento dos clientes jovens utilizam a internet por 70 minutos a cada sessão.
B) mais de 50% dos clientes adultos utilizam a internet por mais de 30 minutos a cada sessão.
C) menos de 5% dos clientes jovens utilizam a internet por mais de 80 minutos a cada sessão.
D) menos de 10% dos clientes adultos utilizam a internet por até 10 minutos a cada sessão.
E) menos de 30% dos clientes adultos utilizam a internet de 30 a 60 minutos a cada sessão.
ENADE 2009 - QUESTÃO 16
Em uma turma de estudantes de Estatística, um professor alega que possui uma moeda viciada, cuja probabilidade, ao jogar cara ou coroa, de sair cara é igual a 0,70.
Os estudantes planejaram o seguinte experimento para verificar a veracidade da afirmação do professor: jogaram a moeda dez mil vezes, anotaram o número de caras e usaram a frequência relativa de caras como uma aproximação para a probabilidade de sair cara nessa moeda.
Esse procedimento é uma aplicação
A) da Lei dos Grandes Números.
B) da Regra da Multiplicação.
C) do Lema de Borel-Cantelli.
D) do Teorema Central do Limite.
E) do Teorema de Bayes.
ENADE 2009 - QUESTÃO 17
Clientes chegam a um balcão de atendimento no horário comercial, segundo um processo de Poisson com média de 6 clientes por hora.
Definindo Tj, como o tempo de chegada do j-ésimo cliente, a diferença entre dois tempos de chegadas consecutivas,  representa o tempo decorrido entre duas chegadas.
representa o tempo decorrido entre duas chegadas.
 representa o tempo decorrido entre duas chegadas.
representa o tempo decorrido entre duas chegadas.Logo, as variáveis aleatórias D1, D2, D3,..., São
A) identicamente distribuídas, mas não independentes.
B) independentes e identicamente distribuídas segundo uma Exponencial.
C) independentes e identicamente distribuídas segundo uma Normal.
D) independentes e identicamente distribuídas segundo uma Poisson.
E) independentes, mas não identicamente distribuídas.
ENADE 2009 - QUESTÃO 18
No hemocentro de uma grande cidade, está havendo falta do sangue tipo AB. Uma pesquisa nessa cidade revelou as seguintes proporções de pessoas em cada tipo sanguíneo:
Se, em um certo dia, dez pessoas, independentemente, se apresentam para doar sangue, a probabilidade de que três doem sangue do tipo A, duas do tipo B, três do tipo AB e duas do tipo O é

ENADE 2009 - QUESTÃO 19
Ana e José conversavam pela internet e resolveram jogar dados. Cada vez que se lança o dado, o jogador ganha 1 ponto, se sair a face 6; e perde 1 ponto, caso sair a face 1. Para as outras faces, a pontuação é nula. Como eles não possuem um dado, resolveram criar um dado virtual honesto.
Dentre as alternativas de código no ambiente computacional R, escolha aquela que simule o jogo proposto. Obs.: a função runif (n, a, b) gera n valores independentes da distribuição Uniforme entre a e b.
ENADE 2009 - QUESTÃO 20
De acordo com um princípio genético simples, se os pais de uma criança têm o genótipo Aa, então há uma probabilidade de 0,25 de que a criança tenha genótipo AA; uma probabilidade de 0,50 de que tenha o genótipo Aa; e de 0,25 de que tenha o genótipo aa.
Uma amostra aleatória de 40 crianças, tendo pais com o genótipo Aa, revelou que 15 crianças tinham o genótipo Aa e 15 tinham o genótipo AA.
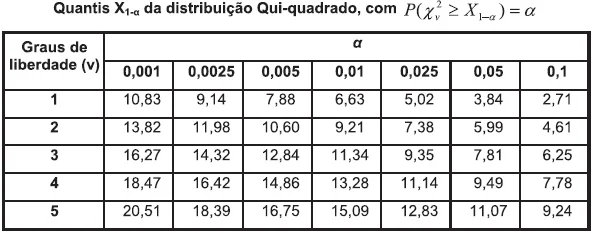
Usando o teste de Qui-quadrado de Aderência e o quadro para verificar esse princípio genético, é CORRETO afirmar que o nível descritivo (valor-p) desse teste
A) é menor que 0,01.
B) é maior do que 0,10.
C) está entre 0,025 e 0,05.
D) está entre 0,01 e 0,025.
E) está entre 0,05 e 0,10.
ENADE 2009 - QUESTÃO 21
Uma pesquisadora está estudando a resistência de um novo material e sabe que essa variável é normalmente distribuída com média p e variância conhecida.
Com base em uma amostra de 20 valores dessa variável, a pesquisadora obteve o seguinte intervalo de 95% confiança para µ:  , em que
, em que  é o valor da média das resistências na amostra coletada.
é o valor da média das resistências na amostra coletada.
 é o valor da média das resistências na amostra coletada.
é o valor da média das resistências na amostra coletada.Escolha a interpretação CORRETA desse intervalo:
A) A probabilidade da resistência assumir um valor dentro do intervalo calculado é 0,95.
B) A probabilidade de o intervalo calculado conter o valor de µ é 0,95.
C) A probabilidade do valor de µ estar dentro do intervalo calculado é próxima de 0,95.
D) Se um grande número de tais intervalos é construído, cada um resultante de uma amostra aleatória de tamanho 20, então 95% deles irão conter o valor  .
.
 .
.E) Se um grande número de tais intervalos é construído, cada um resultante de uma amostra aleatória de tamanho 20, então 95% deles irão conter o valor de µ.
ENADE 2009 - QUESTÃO 23
A pesquisadora encontrou, na literatura, dois estimadores para a proporção p de besouros que morrem após uma hora de exposição ao inseticida:
*  , é a proporção amostral de besouros mortos; e
, é a proporção amostral de besouros mortos; e
 , é a proporção amostral de besouros mortos; e
, é a proporção amostral de besouros mortos; e*  =1, se o primeiro besouro estava morto, e
=1, se o primeiro besouro estava morto, e  =0, caso contrário.
=0, caso contrário.
 =1, se o primeiro besouro estava morto, e
=1, se o primeiro besouro estava morto, e  =0, caso contrário.
=0, caso contrário.Os estimadores  e
e  de p são
de p são
 e
e  de p são
de p sãoA) não viciados, e o erro quadrático médio de  , é menor do que o erro quadrático médio de
, é menor do que o erro quadrático médio de  .
.
 , é menor do que o erro quadrático médio de
, é menor do que o erro quadrático médio de  .
.B) não viciados, e seus erros quadráticos médios são iguais.
C) não viciados, e o erro quadrático médio de  , é maior do que o erro quadrático médio de
, é maior do que o erro quadrático médio de  .
.
 , é maior do que o erro quadrático médio de
, é maior do que o erro quadrático médio de  .
.D) respectivamente, não viciado e viciado, e seus erros quadráticos médios são iguais.
E) respectivamente, viciado e não viciado, e o erro quadrático médio de  , é menor do que o erro quadrático médio de
, é menor do que o erro quadrático médio de  .
.
 , é menor do que o erro quadrático médio de
, é menor do que o erro quadrático médio de  .
.ENADE 2009 - QUESTÃO 24
Um secretário de uma escola, tendo por base uma planilha de 48 notas de uma avaliação de uma turma, com duas casas decimais, resolveu arredondar as notas para o valor inteiro.
Suponha que as diferenças entre a nota original e a arredondada sejam independentes, com distribuição uniforme entre - 0,50 e 0,50, cuja variância é igual a 1/12.
A turma, preocupada com um possível prejuízo devido ao arredondamento, resolveu calcular a probabilidade de que o erro total de arredondamento seja inferior a -3 pontos ou superior a 3 pontos. O valor aproximado obtido para essa probabilidade foi  em que
em que  representa a função de distribuição acumulada da Normal Padrão.
representa a função de distribuição acumulada da Normal Padrão.
 em que
em que  representa a função de distribuição acumulada da Normal Padrão.
representa a função de distribuição acumulada da Normal Padrão.A teoria utilizada pela turma, para calcular essa probabilidade aproximada foi
A) a Desigualdade de Chebyshev, mas ela errou o cálculo do quantil da Normal Padrão.
B) a Lei dos Grandes Números e ela acertou o cálculo do quantil da Normal Padrão.
C) a Lei dos Grandes Números, mas ela errou o cálculo do quantil da Normal Padrão.
D) o Teorema Central do Limite e ela acertou o cálculo do quantil da Normal Padrão.
E) o Teorema Central do Limite, mas ela errou o cálculo do quantil da Normal Padrão.
ENADE 2009 - QUESTÃO 25
Os fenômenos mundiais de crescimento e de declínio florestal atraem grande interesse público e científico. O gráfico a seguir foi baseado nos dados do artigo “Relationship among crown condition, growth and stand nutrition in seven northern Vermont sugarbushes” (Canad. J. of Forest Res., 1995, p. 386.397) que apresenta um diagrama de dispersão do secamento médio dos ramos (%) versus o pH do solo, e os diagramas de caixa (boxplots) das variáveis individualmente. O secamento dos ramos é um indicador de retardamento no crescimento da planta e, quanto mais baixo o pH do solo, maior a sua acidez. A amostra consistiu de 19 pares das medidas tomadas na região.
Analisando-se o gráfico, é CORRETO afirmar que as distribuições de pH do solo e do secamento das plantas apresentam,
A) individualmente, forte assimetria com cauda à esquerda, e pode-se estabelecer uma relação de causa-e-efeito entre as duas variáveis.
B) moderada assimetria com cauda à direita e uma forte associação entre essas duas variáveis.
C) moderada assimetria com cauda à direita, e moderada correlação entre essas duas variáveis.
D) respectivamente, assimetria com cauda à direita e assimetria com cauda à esquerda, e moderada correlação entre essas variáveis.
E) respectivamente, assimetria com cauda à esquerda e assimetria com cauda à direita, e moderada correlação entre essas variáveis.
ENADE 2009 - QUESTÃO 26
A prefeitura de uma cidade quer conhecer o padrão de consumo mensal de energia elétrica e de água de duas de suas regiões: uma delas com residências de alto padrão de construção e outra com residências de baixo padrão de construção.
O Estatístico responsável pelo estudo solicitou, junto às companhias de distribuição de energia elétrica e de água, os valores para o consumo mensal de energia elétrica e de água das residências de uma amostra aleatória de cada região. Por questões de sigilo, as companhias distribuidoras forneceram um resumo dos dados solicitados, a saber, média e desvio-padrão do consumo nas residências amostradas, apresentados na tabela a seguir.
Com base nas informações dessa tabela, o Estatístico conclui que
A) as residências de alto padrão apresentam variabilidade relativa do consumo de água maior do que aquelas de baixo padrão.
B) as residências de alto padrão e de baixo padrão apresentam variabilidades relativas similares quanto vao consumo de energia elétrica.
C) entre as residências de baixo padrão, o consumo de água apresenta variabilidade relativa maior do que a do consumo de energia elétrica.
D) entre as residências de baixo padrão, o consumo de água apresenta variabilidade relativa similar à do consumo de energia elétrica.
E) entre as residências de alto padrão, o consumo de água apresenta variabilidade relativa menor do que a variabilidade relativa do consumo de energia elétrica.
ENADE 2009 - QUESTÃO 27
Um estudante de Estatística gasta muito tempo no ponto de ônibus. Sendo assim, ele registrou seu tempo de espera durante seis meses.
O gráfico mostra o histograma construído a partir desses dados.
Dentre os modelos probabilísticos a seguir, o que NÃO é adequado para explicar esses dados, sem o uso de transformação, é
A) Exponencial.
B) F de Snedecor.
C) Log-normal.
D) Normal.
E) Weibull.
ENADE 2009 - QUESTÃO 28
Considere as seguintes funções de densidade de probabilidade conjuntas ou funções de probabilidade conjuntas:
Entre essas funções, aquelas que caracterizam um par de variáveis aleatórias independentes são
A) I e III.
B) I e IV.
C) II e III.
D) II e IV.
E) III e IV.
ENADE 2009 - QUESTÃO 29
Um biólogo deseja estimar o tamanho da população de animais de uma espécie numa região. O Estatístico consultado indicou o método de Captura e Recaptura, e explicou que o procedimento consiste em capturar r animais, da espécie desejada, sem reposição, e marcá-los.
Em seguida, os animais serão soltos e espera-se um tempo para permitir que se misturem aos demais. Uma segunda amostra de n animais é retirada, sem reposição, e o número de animais marcados é contado.
Supondo que o tamanho dessa população é N e considerando que o processo de marcação não altera a aleatoriedade da segunda amostra, o número de animais marcados encontrados na segunda amostra comporta-se segundo a distribuição
A) Binomial com parâmetros n e p=r/N.
B) Binomial Negativa com parâmetros n+1 e p=r/N.
C) Geométrica com parâmetro p=r/N.
D) Hipergeométrica com parâmetros N, r e n.
E) Poisson com parâmetro nr/N.
ENADE 2009 - QUESTÃO 30
Um técnico de controle de qualidade de uma mineração coletou amostras do minério extraído em certo dia para avaliar o teor de ferro (em %). Com o objetivo de verificar se o minério atende aos padrões de qualidade, o Estatístico da equipe estimou o teor médio de ferro da produção daquele dia, usando um intervalo de 95% de confiança. O intervalo obtido foi [60,88% ; 61,71%].
O técnico avaliou esse intervalo como sendo muito amplo para se fazer uma inferência sobre a qualidade do minério amostrado.
Para diminuir a amplitude do intervalo, mantendo o mesmo nível de confiança, o Estatístico da equipe deve sugerir ao técnico da qualidade que
A) aumente o número de amostras de minério e fixe um erro de estimação menor.
B) aumente o número de amostras de minério e reduza a probabilidade de rejeitar a produção do dia erroneamente.
C) aumente o número de amostras de minério e verifique se existem fontes de variação que podem ser minimizadas.
D) mantenha o tamanho de amostra fixo e aumente o poder do teste.
E) mantenha o tamanho de amostra fixo e reduza a probabilidade de rejeitar a produção do dia erroneamente.
ENADE 2009 - QUESTÃO 31
Um Estatístico está construindo um modelo para previsão de risco de crédito para um banco. Esse modelo será utilizado para conceder ou negar crédito a um cliente correntista. A base de dados históricos da carteira de clientes revelou que 40.000 contratos foram pagos em dia ou com atraso de até 30 dias (adimplentes) e 10.000 contratos tiveram atraso superior a 30 dias (inadimplentes).
Por questões de custo de computação, o Estatístico poderá trabalhar somente com 5.000 contratos. Assim, ele considera todos os 50.000 contratos como a população alvo. Os contratos estão numerados sequencialmente de 1 a 50.000, sendo que os primeiros 40.000 correspondem aos adimplentes. Ele quer estimar a média da idade do financiado. Da experiência prévia, ele sabe que os inadimplentes são, em geral, mais jovens do que os adimplentes.
Com o objetivo de reduzir o erro-padrão do estimador da média da idade do financiado, o procedimento adequado para selecionar a amostra é

ENADE 2009 - QUESTÃO 32
Um hematologista quer verificar se a dieta tem influência no tempo de coagulação do sangue (em segundos) de uma espécie de animal. Para isso, 24 animais foram divididos aleatoriamente em quatro grupos, que receberam diferentes dietas, denotadas por A, B, C e D. Verificadas as condições necessárias para o uso da técnica de Análise de Variância, sua aplicação originou as tabelas.
Com base nesses resultados, o hematologista conclui que
A) a diferença observada entre os tempos médios de coagulação é estatisticamente significante para pelo menos duas dietas.
B) a estimativa do desvio-padrão do tempo de coagulação para uma dada dieta é maior do que 3 segundos.
C) a proporção da variação total nos tempos de coagulação, que é explicada pela variação na dieta, é menor do que 0,50.
D) o tempo médio de coagulação da dieta A é estatisticamente diferente dos tempos médios de coagulação das demais dietas.
E) o tempo médio de coagulação das dietas B e C é igual a 5 e 7 segundos, respectivamente.
ENADE 2009 - QUESTÃO 33
O gerente de uma rede de concessionárias de automóveis novos deseja estudar a relação entre o gasto com acessórios no ato da compra do automóvel (Y, em reais) em função do valor do automóvel (X1, em reais), do sexo do comprador (X2 = 0, se feminino; X2= 1, se masculino) e da idade do comprador (X3, em anos completos).
O Estatístico consultado para resolver esse problema selecionou uma amostra aleatória de vendas, ajustou um modelo de regressão linear usando essas variáveis e apresentou ao gerente as conclusões:
I. O gasto com acessórios cresce linearmente com o valor do automóvel.
II. As mulheres gastam menos com acessórios do que os homens.
III. O gasto com acessórios decresce linearmente com a idade do comprador.
IV. O efeito linear do valor do automóvel no gasto com acessórios não é o mesmo nos dois sexos.
V. O efeito linear do valor do automóvel no gasto com acessórios não é o mesmo para qualquer idade do comprador (e vice-versa).
VI. O efeito linear da idade do comprador no gasto com acessórios é o mesmo nos dois sexos.
Considerando-se essas conclusões, o modelo final apresentado ao gerente foi do tipo.

O enunciado abaixo deve ser utilizado para responder as questões 34 e 35
Uma pesquisa investigou a lucratividade de bancos, informando a variação percentual de dos lucros entre a primeira metade do último ano e a primeira metade do ano atual. De experiências prévias, sabe-se que essa variação percentual segue uma distribuição Normal com desvio padrão conhecido  . O pesquisador quer verificar se houve ou não mudanças no lucro entre os períodos considerados. Para isso, formulou as hipóteses H0 : µ = 0 vs H1 : µ ≠ 0 , em que µ representa a variação percentual média dos bancos. Com base numa amostra aleatória de n bancos, foi proposto o seguinte procedimento de teste:
. O pesquisador quer verificar se houve ou não mudanças no lucro entre os períodos considerados. Para isso, formulou as hipóteses H0 : µ = 0 vs H1 : µ ≠ 0 , em que µ representa a variação percentual média dos bancos. Com base numa amostra aleatória de n bancos, foi proposto o seguinte procedimento de teste:
 . O pesquisador quer verificar se houve ou não mudanças no lucro entre os períodos considerados. Para isso, formulou as hipóteses H0 : µ = 0 vs H1 : µ ≠ 0 , em que µ representa a variação percentual média dos bancos. Com base numa amostra aleatória de n bancos, foi proposto o seguinte procedimento de teste:
. O pesquisador quer verificar se houve ou não mudanças no lucro entre os períodos considerados. Para isso, formulou as hipóteses H0 : µ = 0 vs H1 : µ ≠ 0 , em que µ representa a variação percentual média dos bancos. Com base numa amostra aleatória de n bancos, foi proposto o seguinte procedimento de teste:ENADE 2009 - QUESTÃO 34
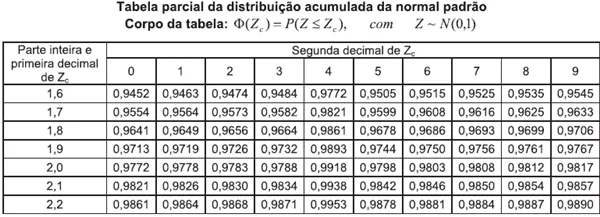
Usando a tabela a seguir, assinale a opção que fornece o nível de significância desse teste.
A) 0,0100.
B) 0,0114.
C)0,0228.
D) 0,0456.
E) 0,0500.
ENADE 2009 - QUESTÃO 36
A taxa X de gordura corporal (massa de gordura dividida pela massa total) de mulheres adultas tem distribuição Beta com parâmetros 1 e θ, com θ > O, cuja função de densidade de probabilidade é
Seja X1,X2,...,Xn uma amostra aleatória simples de mulheres adultas dessa região.
O estimador de máxima verossimilhança de θ é

ENADE 2009 - QUESTÃO 37
Uma empresa de refrigerantes enche garrafas especificadas para conter dois litros da bebida. O processo de envasamento é mecanizado. Sendo assim, existe uma variação no volume que é dispensado pela máquina.
Para evitar desperdício da bebida ou garrafas com volume muito abaixo do especificado, o Estatístico responsável pelo controle de qualidade da empresa acompanha, diariamente, esse processo de produção. Para tanto, a cada dia, ele seleciona uma amostra aleatória de 50 garrafas envasadas e mede o volume de seu conteúdo.
A figura a seguir mostra os resultados das amostras de sete dias consecutivos, resumidos em boxplots (diagramas de caixa ou desenhos esquemáticos). Os resultados do 1º dia mostram um processo de envasamento satisfatório. Ao final do 4º dia foi feito um ajuste nas máquinas envasadoras.
Considere as seguintes afirmativas baseadas na figura:
A1. O volume mediano manteve-se próximo do valor nominal até o 4º dia.
A2. O processo do 2º ao 4º dias não pode ser considerado satisfatório.
A3. O ajuste feito nas máquinas ao final do 4º dia teve o efeito de retornar a variabilidade do processo ao nível considerado satisfatório.
A4. O processo no 5º e no 6º dias não pode ser considerado satisfatório.
Considere as possíveis justificativas para as afirmativas acima (não necessariamente na mesma ordem):
R1. porque a distância interquartílica dos volumes está próxima ao valor considerado satisfatório.
R2. porque o traço horizontal dentro das caixas dos boxplots está próximo ao valor de 2000 ml
R3. porque o valor mediano dos volumes está abaixo do especificado.
R4. porque a variabilidade dos volumes despendidos cresceu.
Escolha a alternativa que associa as afirmativas com suas justificativas corretas:
A) A1 com R2; A2 com R3.
B) A1 com R2; A3 com R1.
C) A1 com R4; A3 com R1.
D) A2 com R2; A4 com R3.
E) A2 com R4; A4 com R4.











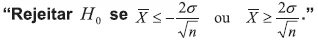








COMENTÁRIOS