Prova de Matemática ENADE 2008 com Gabarito

Prova de Matemática ENADE 2008 com Gabarito

Prova de Matemática ENADE 2008 com Gabarito

OBS: As questões objetivas de 01 a 08 estão disponível na prova de Formação Geral que você pode acessar clicando neste link. As questões discursivas não foram disponibilizadas com padrão de resposta.

QUESTÃO 11

ENADE: Em um jogo de futebol, um jogador irá bater uma falta diretamente para o gol. A falta é batida do ponto P, localizado a  12 metros da barreira. Suponha que a trajetória da bola seja uma parábola, com ponto de máximo em Q, exatamente acima da barreira, a 3 metros do chão, como ilustra a figura abaixo.

Sabendo-se que o gol está a 8 metros da barreira, a que altura está a bola ao atingir o gol?

GABARITO. 

QUESTÃO 12

ENADE: No plano cartesiano xOy, as equações x²+ y² + y = 0 e x² - y - 1 = 0 representam uma circunferência Γ e uma parábola P, respectivamente. Nesse caso,

A) a reta de equação y = -1 é tangente às curvas Γ e P.

B) as curvas Γ e P têm mais de um ponto em comum.

C) existe uma reta que passa pelo centro de Γ e que não intercepta a parábola P.

D) o raio da circunferência Γ é igual a 1.

E) a parábola P tem concavidade voltada para baixo.

GABARITO.

QUESTÃO 13

ENADE: Há 10 postos de gasolina em uma cidade. Desses 10, exatamente dois vendem gasolina adulterada. Foram sorteados aleatoriamente dois desses 10 postos para serem fiscalizados. Qual é a probabilidade de que os dois postos infratores sejam sorteados?

GABARITO. 

QUESTÃO 14

ENADE: Assinale a opção que contém o sistema de inequações que determina a região triangular PQR desenhada abaixo.

GABARITO. 

QUESTÃO 15

ENADE: Uma professora do ensino fundamental resolveu utilizar, em suas aulas, a construção de um avião de papel para explorar alguns conceitos e propriedades da geometria plana.

Utilizando uma folha de papel retangular, os estudantes deveriam começar fazendo as dobras na folha ao longo dos segmentos de reta indicados na figura ao lado.

As seguintes condições, segundo instruções da professora, devem ser satisfeitas:

< a reta determinada por M e U é a mediatriz do segmento AB;

< AC, BD e AB são segmentos congruentes;

< PT e TQ são segmentos congruentes;

< PD e BD são segmentos congruentes.

A partir da análise da figura, um estudante afirmou o seguinte:

O triângulo PQD é obtusângulo

porque

o triângulo PQT é equilátero.

Com relação ao que foi afirmado pelo estudante, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, e a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 16

ENADE: A concentração de certo fármaco no sangue, t horas após sua administração, é dada pela fórmula:

Em qual intervalo essa função é crescente?

A) t ≥ 0

B) t > 10

C) t > 1

D) 0 ≤ t < 1

GABARITO.

QUESTÃO 17

ENADE: No plano complexo, a área do triângulo de vértices  

GABARITO. 

QUESTÃO 18

ENADE: No anel dos inteiros módulo 12, R = Z /12Z,

A) não há divisores de zero.

B) todo elemento não-nulo é inversível.

C) o subconjunto dos elementos inversíveis forma um subanel de R.

D) a multiplicação não é comutativa.

E) há exatamente 4 elementos inversíveis.

GABARITO.

QUESTÃO 19

ENADE: Considere g : R →  R  uma função com derivada  

contínua e f a função definida por  

 para todo x , R.

Nessas condições, avalie as afirmações que se seguem.

I A função f é integrável em todo intervalo [a, b], a, b ꞓ R, a < b.

II A função f é derivável e sua derivada é a função g.

III A função diferença f ! g é uma função constante.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e II

GABARITO.

QUESTÃO 20

ENADE: Para cada número real x, considere o conjunto Cx formado por todos os números obtidos somando-se a x um número racional, isto é,

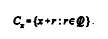
Sob essas condições, conclui-se que

A) o número π pertence ao conjunto C1 .

B) o conjunto C4 ꓵ C5 possui um único elemento.

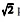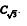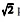C) o número  pertence ao conjunto  .

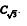D) os conjuntos C3 e C⅓ são iguais.

E) o número zero pertence ao conjunto .

GABARITO.

QUESTÃO 21

ENADE: Para que valores de k e m o polinômio P(x) = x³ – 3x² + kx + m é múltiplo de Q(x) = x² – 4?

A) k = - 4 e m = 12

B) k = - 3 e m = - 4

C) k = - 3 e m = - 12

D) k = - 4 e m = - 3

E) k = - 2 e m = 2

GABARITO.

QUESTÃO 22

ENADE: Uma transformação linear T: R² → R²  faz uma reflexão em relação ao eixo horizontal, conforme mostrado na figura a seguir.

Essa transformação T

A) é dada por T(x, y) = (- x, y).

B) tem autovetor (0, - 1) com autovalor associado igual a 2.

C) tem autovetor (2, 0) com autovalor associado igual a 1.

D) tem autovalor de multiplicidade 2.

E) não é inversível.

GABARITO.

QUESTÃO 23

ENADE: Considere o sistema de equações a seguir.

Analise as asserções seguintes relativas à resolução desse sistema de equações lineares.

O sistema não tem solução

porque

o determinante da matriz dos coeficientes é igual a zero.

A respeito dessa afirmação, assinale a opção correta.

A) As duas asserções são proposições verdadeiras e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 24

ENADE: Considere que Q1 = {r1, r2, r3, ...} seja uma enumeração de todos os números racionais pertencentes ao intervalo [0, 1] e que, para cada número inteiro i > 1, Ii  denote o intervalo aberto    cujo comprimento é li . Qual é a soma da série  

GABARITO. 

QUESTÃO 25

ENADE: O projeto de construção de uma peça de artesanato foi realizado utilizando-se um software geométrico que permite interceptar um tetraedro regular com planos.

A figura a seguir mostra o tetraedro RSTU e três pontos M, N e P do plano α de interseção.

Sabendo que M, N e P são pontos médios de SR, SU e ST, respectivamente, e que o tetraedro RSTU tem volume igual a 1, avalie as seguintes afirmações.

I O volume da pirâmide SMNP é igual  .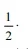 

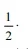II A interseção do plano a com o tetraedro é um paralelogramo.

III As retas que contêm as arestas MP e RU são reversas.

É correto o que se afirma em

A) I, apenas.

B) III, apenas.

C) I e II, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

QUESTÃO 26

ENADE: Analisando a função f(x, y) = x² (x - 1) + y(2x - y), definida no domínio D = {(x, y) 0 R² ; -1 < x < 1, - 1 < y < 1}, um estudante de cálculo diferencial escreveu o seguinte:

A função f tem um ponto de mínimo global em D

porque

o ponto (0, 0) é um ponto crítico de f.

A respeito da afirmação feita pelo estudante, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 27

ENADE: Qual é o resto da divisão de ²³³4 por 23?

A) 2

B) 4

C) 8

D) 16

E) 20

GABARITO.

QUESTÃO 28 - RESOLUÇÃO NÃO ENCONTRADA

QUESTÃO 29 - RESOLUÇÃO NÃO ENCONTRADA

LICENCIATURA

QUESTÃO 30

ENADE: As potencialidades pedagógicas da história no ensino de matemática têm sido bastante discutidas. Entre as justificativas para o uso da história no ensino de matemática, inclui-se o fato de ela suscitar oportunidades para a investigação. Considerando essa justificativa, um professor propôs uma atividade a partir da informação histórica de que o famoso matemático Pierre Fermat [1601-1665], que se interessava por números primos, percebeu algumas relações entre números primos ímpares e quadrados perfeitos.

Para que os alunos também descobrissem essa relação, pediu que eles completassem a tabela a seguir, verificando quais números primos ímpares podem ser escritos como soma de dois quadrados perfeitos. Além disso, solicitou que observassem alguma propriedade comum a esses números.

A partir da atividade de investigação proposta pelo professor, analise as afirmações seguintes.

I Todo número primo da forma 4n + 1 pode ser escrito como a soma de dois quadrados perfeitos.

II Todo número primo da forma 4n + 3 pode ser escrito como a soma de dois quadrados perfeitos.

III Todo número primo da forma 2n + 1 pode ser escrito como a soma de dois quadrados perfeitos.

Está correto o que se afirma em

A) I, apenas. 

B) II, apenas. 

C) I e III, apenas.

E) I, II e III.

D) II e III, apenas.

GABARITO.

QUESTÃO 31

ENADE: Na discussão relativa a funções exponenciais, um professor propôs a seguinte questão: Para que valores não-nulos de k e m a função f(x) = mekx é uma função crescente? 

Como estratégia de trabalho para que os alunos respondam à questão proposta, é adequado e suficiente o professor sugerir que os alunos

A) considerem m = 1 e k = 1, utilizem uma planilha eletrônica para calcular valores da função f em muitos pontos e comparem os valores obtidos.

B) considerem m = 1 e k = 1, m = -1 e k = 1, esbocem os gráficos da função f e, em seguida, comparem esses dois gráficos.

C) formem pequenos grupos, sendo que cada grupo deve esboçar o gráfico de uma das funções  

 , para m = 1, 2, 3, 4 ou 5, e comparem, em seguida, os gráficos encontrados.

D) esbocem os gráficos das funções y = ex  e y = e ͯ  e analisem o que acontece com esses gráficos quando a variável e a função forem multiplicadas por constantes positivas ou negativas. 

E) construam uma tabela com os valores de f para x número inteiro variando de -5 a 5, fixando m = 1 e k = 1 e, em seguida, comparem os valores encontrados.

GABARITO.

QUESTÃO 32

ENADE: A Matemática no ensino médio tem papel formativo — contribui para o desenvolvimento de processos de pensamento e para a aquisição de atitudes — e caráter instrumental — pode ser aplicada às diversas áreas do conhecimento —, mas deve ser vista também como ciência, com suas características estruturais específicas. 

OCNEM (com adaptações).

Ao planejar o estudo de funções no ensino médio, o(a) professor(a) deve observar que

A) o objetivo do estudo de exponenciais é encontrar os zeros dessas funções.

B) as funções logarítmicas podem ser usadas para transformar soma em produto.

C) as funções trigonométricas devem ser apresentadas após o estudo das funções exponenciais.

D) a função quadrática é exemplo típico de comportamento de fenômenos de crescimento populacional.

E) o estudo de funções polinomiais deve contemplar propriedades de polinômios e de equações algébricas.

GABARITO.

QUESTÃO 33

ENADE: A professora Clara propôs a seus alunos que encontrassem a solução da seguinte equação do segundo grau: x² 1 = (2x + 3)(x - 1)

Pedro e João resolveram o exercício da seguinte maneira.

Pedro e João perguntaram à professora por que encontraram soluções diferentes. A professora observou que outros alunos haviam apresentado soluções parecidas com as deles.

Entre as estratégias apresentadas nas opções a seguir, escolha a mais adequada a ser adotada por Clara visando à aprendizagem significativa por parte dos alunos.

A) Indicar individualmente, para cada aluno que apresentou uma resolução incorreta, onde está o erro e como corrigi-lo, a partir da estratégia inicial escolhida pelo aluno.

B) Resolver individualmente o exercício para cada aluno, usando a fórmula da resolução da equação do 2.º grau, mostrando que esse é o método que fornece a resposta correta.

C) Pedir a Pedro e João que apresentem à classe suas soluções para discussão e estimular os alunos a tentarem compreender onde está a falha nas soluções apresentadas e como devem fazer para corrigi-las.

D) Escrever a solução do exercício no quadro, usando a fórmula da resolução da equação do 2.º grau, para que os alunos percebam que esse é o método que fornece a resposta correta.

E) Pedir que cada um deles comunique à classe como resolveu o exercício e, em seguida, explicar no quadro para a turma onde está a falha na resolução de cada um e como eles devem fazer para corrigi-la.

GABARITO.

QUESTÃO 34

ENADE: Observe a seguinte atividade de construções geométricas.

• Construir um triângulo ABC  qualquer.

• Traçar a bissetriz do ângulo   e, em seguida, a  bissetriz do ângulo   . 

• Marcar o ponto de encontro dessas duas bissetrizes.

• Traçar a bissetriz do ângulo . 

O que você observa? 

Será que, se você recomeçar a construção a partir de outro triângulo, chegará à mesma observação?

O uso de um software de geometria dinâmica na execução dessa atividade e de outras similares

A) pode mostrar que o estudo das construções com régua e compasso é desnecessário.

B) dispensa a demonstração dos resultados encontrados pelos alunos.

C) prejudica o desenvolvimento do raciocínio lógico-dedutivo.

D) dificulta o desenvolvimento do pensamento geométrico.

E) pode contribuir para a elaboração de conjecturas pelos alunos.

GABARITO.

QUESTÃO 35

ENADE: Algumas civilizações utilizavam diferentes métodos para multiplicar dois números inteiros positivos. Por volta de 1400 a.C., os egípcios utilizavam uma estratégia para multiplicar dois números que consistia em dobrar e somar.

Por exemplo, para calcular 47 × 33, o método pode ser descrito do seguinte modo:

• escolha um dos fatores; por exemplo, 47;

• na 1.ª linha de uma tabela, escreva o número 1 na 1.ª coluna e o fator escolhido, na 2.ª coluna;

• em cada linha seguinte da tabela, escreva o dobro dos números da linha anterior, até encontrar, na 1.ª coluna, o menor número cujo dobro seja maior ou igual ao outro fator, no caso, 33;

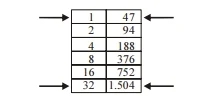
• selecione os números da 1.ª coluna cuja soma seja igual a 33, conforme indicado na tabela, ou seja, 1 + 32 = 33;

• adicione os números correspondentes da 2.ª coluna, ou seja, 47 + 1.504 = 1.551;

• tome como resultado da multiplicação o valor 1.551.

Com base nessas informações, analise as asserções a seguir.

Utilizando o método egípcio, é possível multiplicar quaisquer dois números inteiros positivos, porque todo número inteiro positivo pode ser escrito como uma soma de potências de 2.

A respeito dessa afirmação, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 36

ENADE: A figura abaixo mostra alguns segmentos construídos em um geoplano por um estudante, de acordo com a orientação dada pela professora.

Acerca do uso do geoplano retangular nessa atividade, assinale a opção incorreta.

A) O geoplano auxilia na compreensão de que   .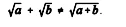

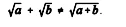B O geoplano auxilia na compreensão de que    .

C) O geoplano auxilia na representação geométrica de números irracionais da forma .

D) O geoplano auxilia na obtenção da relação entre o comprimento de uma circunferência e seu diâmetro.

E) O geoplano auxilia na simplificação de expressões com irracionais algébricos, como, por exemplo,.

GABARITO.

QUESTÃO 37

ENADE: Segundo os parâmetros curriculares nacionais, todas as disciplinas escolares devem contribuir com a construção da cidadania. Refletindo sobre esse tema, avalie as asserções a seguir.

Uma forma de o ensino da Matemática contribuir com a formação do cidadão é o professor propor situações-problema aos alunos, pedir que eles exponham suas soluções aos colegas e expliquem a estratégia de resolução utilizada, estimulando o debate entre eles,

porque

os alunos, ao expor seu trabalho para os colegas, ouvir e debater com eles as diferentes estratégias utilizadas, são estimulados a justificar suas próprias estratégias, o que contribui com o desenvolvimento da autonomia, estimula a habilidade de trabalhar em coletividade e a respeitar a opinião do outro, características fundamentais de um cidadão crítico e consciente.

A respeito dessa afirmação, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 38

ENADE: Entre os procedimentos envolvidos na modelagem de uma situação-problema, estão sua tradução para a linguagem matemática e a resolução do problema, utilizando-se conhecimentos matemáticos. Nessa perspectiva, um professor propôs a seguinte situação-problema para seus alunos:

Escolha o nome para uma empresa que possa ser lido da mesma forma de qualquer um dos lados de uma porta de vidro transparente.

A solução desse problema pressupõe encontrar

A) letras do alfabeto que sejam simétricas em relação a um ponto.

B) letras do alfabeto que tenham simetria em relação a um eixohorizontal.

C) letras do alfabeto que tenham simetria em relação a um eixo vertical.

D) palavras que sejam simétricas em relação a um ponto.

E) palavras que sejam simétricas em relação a um eixo horizontal.

GABARITO.

QUESTÃO 39

ENADE: As questões I e II abaixo fizeram parte das provas de Matemática do Sistema de Avaliação da Educação Básica (SAEB), em 2003, para participantes que terminaram, respectivamente, a 8.ª série do ensino fundamental e o 3.º ano do ensino médio.

Na questão I, 56% dos participantes escolheram como correta a opção C, enquanto, na questão II, 61% dos participantes escolheram como correta a opção A.

Analisando os dados apresentados, assinale a opção que não justifica o erro que os estudantes cometeram ao escolher as suas respostas.

A Na questão I, a maioria dos respondentes considera que a representação do número decimal 0,ab na forma de fração é  .

B) Nas questões I e II, a maioria dos respondentes considera que as frações e   são equivalentes.

C) Na questão I, a maioria dos respondentes considera que 0,25 e   são representações de números diferentes.

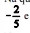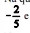D) Na questão II, a maioria dos respondentes considera que  e - 0,4 são representações de números diferentes.

E) Na questão II, a maioria dos respondentes considera que a representação decimal da fração 
é a,b.

GABARITO.

QUESTÃO 40 - RESOLUÇÃO NÃO ENCONTRADA

QUESTÃO 41

ENADE: O cilindro e o catenóide, representados nas figuras I e II, são superfícies regulares de rotação geradas, respectivamente, pelas curvas α1(t) = (1, 0, t) e α2(t) = (cosht, 0, t), com t ꞓ R.

Considerando essas informações, conclui-se que

A) a curvatura gaussiana do catenóide é negativa.

B) as duas superfícies são localmente isométricas.

C) as únicas geodésicas do cilindro são as retas.

D) a curvatura gaussiana do cilindro é constante e positiva.

E) as curvas α1(t) e α2(t) são os paralelos das respectivas superfícies de rotação.

GABARITO.

QUESTÃO 42

ENADE: Um domínio de integridade é um domínio principal quando todo ideal é principal, isto é, pode ser gerado por um único elemento.

Com base nesse conceito, avalie as seguintes afirmações.

I O anel Z[x] — de polinômios sobre Z na variável x — é um domínio principal, em que Z é o anel dos inteiros.

II Se K é um corpo, K[x] — o anel de polinômios sobre K na variável x — é um domínio principal.

III O anel dos inteiros gaussianos Z[i] é um domínio principal.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

QUESTÃO 43

ENADE: Considere o espaço vetorial V = (R² , < , >1) munido do seguinte produto interno: <u, v>1 = x1x2 - y1x2 - x1y2 + 4y1y2, em que v = (x1, y1) e u = (x2, y2) são vetores de ú2 . Considere T : V → V o operador linear dado por  . Com relação ao produto interno < , >1 e ao operador T, assinale a opção correta.

A) Os vetores e1 = (1, 0) e e2 = (0, 1) são ortogonais em relação ao produto interno < , >1.

B) O operador T preserva o produto interno, isto é, <T(u), T(v) >1 = < u, v >1. 

C) T(x, y) = T(y, x), para todo (x, y) de R² .

D) O vetor u = (2, 0) pertence ao núcleo de T.

E) Existe um vetor v = (x, y) 0 R²  tal que x2  + y2  = 1 e <v, v>1 = 0.

GABARITO.

QUESTÃO 44

ENADE: Para cada número real k, a equação diferencial yO(x) + 2yN(x) + ky(x) = 0 possui uma única solução yk(x) que satisfaz às condições iniciais  . 

Considere o limite   e analise as seguintes asserções a respeito desse limite.

Para qualquer k 0 (0, 1), o valor de Lk é zero

porque

a equação diferencial dada é não-linear.

A respeito dessa afirmação, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, e a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 45

ENADE: Considere uma função f : R → R  que possui segunda derivada em todo ponto e que satisfaz à seguinte propriedade:

Um estudante de cálculo diferencial, ao deparar-se com essa situação, escreveu a afirmação seguinte.

A segunda derivada f O(2) = 1

porque 

  , qualquer que seja a função g.

Com relação ao afirmado pelo estudante, assinale a opção correta.

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.

B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.

C) A primeira asserção é uma proposição verdadeira, e a segunda é falsa.

D) A primeira asserção é uma proposição falsa, e a segunda é verdadeira.

E) Ambas as asserções são proposições falsas.

GABARITO.

QUESTÃO 46

ENADE: Considere as integrais complexas

A soma I1 + I2 é igual a

A) 4π.

B) 2π.

C) 0.

D) - 2π.

E) 4π.

GABARITO.

QUESTÃO 47

ENADE: Considere o grupo G das raízes 6-ésimas da unidade, isto é, o grupo formado pelos números complexos z, tais que z¬ = 1. Com relação ao grupo G, assinale a opção correta.

A) O grupo G é cíclico.

B) G é um grupo de ordem 3.

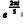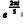C) O número complexo   é um elemento primitivo de G.

D) Existe um subgrupo de G que não é cíclico.

E) Se z é um elemento primitivo de G, então z 2  também é um elemento primitivo de G.

GABARITO.

QUESTÃO 48

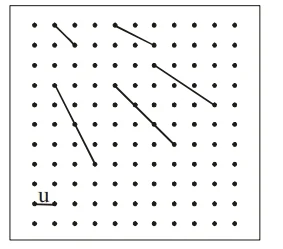
ENADE: No plano R² , considere que o conjunto Q consiste dos lados de um quadrado de lado unitário. Nesse conjunto, pode-se definir uma métrica d da seguinte maneira: dados dois pontos distintos, A, B ꞓ Q, d(A, B) é definida como o comprimento euclidiano da menor poligonal contida em Q e com extremidades A e B, e d(A, B) = 0, se A = B, conforme ilustra a figura abaixo.

O espaço métrico Q, munido da métrica d,

A) tem diâmetro igual a   .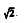

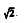B) possui um par de pontos tais que d(x, y) ≠ d(y, x).

C) é um subespaço métrico do plano R²  munido da métrica euclidiana.

D) coincide com uma bola aberta de centro em um dos vértices de Q e de raio 3 na métrica d.

E) é igual à união de duas bolas abertas de centros em vértices distintos de Q e de raio 1 na métrica d.

GABARITO.

QUESTÃO 49

ENADE: Quando uma partícula desloca-se ao longo de uma curva C parametrizada por r(t) = (x(t), y(t), z(t)), t 0 [a, b], sob a ação de um  campo de força   em R³, o trabalho realizado pelo campo ao longo de C é dado por

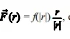Se   , em que f : R → R é uma função contínua e |r| =    = grad(g(|r|)), em que g é uma primitiva de f. Considerando essas informações, conclui-se que o trabalho realizado pelo campo  ao longo da hélice C dada por r(t) = (cos t, sen t, t), t 0 [0, 2π], é

GABARITO. 

QUESTÃO 50

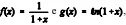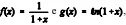ENADE: Efetuando-se o produto das séries de Taylor, em torno da origem, das funções reais   e , obtém-se, para |x| < 1, o desenvolvimento em série de potências da seguinte função:

O coeficiente de xᴺ  na série de potências de φᴺ, a derivada de primeira ordem da função φ, é igual a

GABARITO.