Prova de Matemática ENADE 2011 com Gabarito OBS: As questões objetivas de 01 a 08 estão disponível na ...
Prova de Matemática ENADE 2011 com Gabarito
OBS: As questões objetivas de 01 a 08 estão disponível na
prova de Formação Geral que você pode acessar
clicando neste link. As questões discursivas não foram disponibilizadas com padrão de
resposta.
ENADE 2011 - QUESTÃO 09
Considere o sistema de equações lineares Ax = b, com m equações e n incógnitas. Supondo que a solução do sistema homogêneo correspondente seja, única, avalie as afirmações a seguir.
I. As colunas da matriz A são linearmente dependentes.
II. O sistema de equações lineares Ax = b tem infinitas soluções.
III. Se m > n, então a matriz A tem m - n linhas que são combinações lineares de n linhas.
IV. A quantidade de equações do sistema Ax = b é maior ou igual à quantidade de incógnitas.
São corretas apenas as afirmações
A) I e II.
B) II e III.
C) III e IV.
D) I, II e IV.
E) I, III e IV.
ENADE 2011 - QUESTÃO 11
Considere os elementos  pertencentes ao grupo das permutações S3 .
pertencentes ao grupo das permutações S3 .
 pertencentes ao grupo das permutações S3 .
pertencentes ao grupo das permutações S3 .Assinale a opção que representa αβ.

ENADE 2011 - QUESTÃO 12
O matemático grego Hipócrates de Chios (470 a. C. – 410 a. C.) é conhecido como um excelente geômetra. Ele calculou a área de várias regiões do plano conhecidas como lúnulas, que são limitadas por arcos de circunferência, com centros e raios diferentes.
As figuras I e II a seguir mostram, respectivamente, as lúnulas L1 e L2, limitadas por um arco de circunferência de centro O e raio r e por semicircunferências cujos diâmetros são o lado de um hexágono regular e o lado de um quadrado inscritos na circunferência de raio r e centro O.
Considerando r um número racional, avalie as asserções a seguir.
A razão entre as áreas A1 e A2 das lúnulas L1 e L2 é um número racional.
PORQUE
A1 e A2 podem ser, respectivamente, representadas por π x q1 e π x q2, em que q1 e q2 são números racionais.
A respeito dessas asserções, assinale a opção correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 13
O conjunto dos números complexos pode ser representado geometricamente no plano cartesiano de coordenadas xOy por meio da seguinte identificação:
z = x + iy ➝ P = (x, y)
Nesse contexto, analise as afirmações a seguir.
I. As soluções da equação z = 1 são vértices de um quadrado de lado 1.
II. A representação geométrica dos números z complexos tais que |z| = 1 é uma circunferência com centro na origem e raio 1.
III. A representação geométrica dos números complexos z tais que é uma reta que tem coeficiente angular igual a  radianos.
radianos.
 radianos.
radianos.É correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
ENADE 2011 - QUESTÃO 14
Em um plano de coordenadas cartesianas xOy, representa-se uma praça de área P, que possui em seu interior um lago de área L, limitado por uma curva C fechada, suave, orientada no sentido contrário ao dos ponteiros de um relógio.
Considere que, sobre o lago, atua um campo de forças F(x,y) = yi + xj. Supondo que T representa o trabalho realizado por F(x,y) para mover uma partícula uma vez ao longo da curva C e que, comparando-se apenas os valores numéricos das grandezas, a área não ocupada pelo lago é igual a  conclui-se que
conclui-se que
 conclui-se que
conclui-se queA) P = T.
B) T = L.
C) P = 2T.
D) T = 4L.
E) P = 4L.
ENADE 2011 - QUESTÃO 15
Para tentar liquidar o estoque de televisores cujo valor oferecido no crédito, após acréscimo de 20% sobre o valor da tabela, era de R$ 1 320,00, uma loja lançou uma nova campanha de vendas que ofereceu as seguintes condições promocionais, com base no valor da tabela:
I. uma entrada de 25%, e o restante em cinco parcelas iguais mensais; ou
II. uma entrada de 60%, e o restante em oito parcelas iguais mensais.
O cliente que comprar o televisor nessa promoção pagará em cada parcela
A) R$ 55,00, se escolher a opção II.
B) R$ 66,00, se escolher a opção I.
C) R$ 192,50, se escolher a opção II.
D) R$ 198,00, se escolher a opção II.
E) R$ 275,00, se escolher a opção I.
ENADE 2011 - QUESTÃO 16
Suponha que um instituto de pesquisa de opinião pública realizou um trabalho de modelagem matemática para mostrar a evolução das intenções de voto nas campanhas dos candidatos Paulo e Márcia a governador de um Estado, durante 36 quinzenas.
Os polinômios que representam, em porcentagem, a intenção dos votos dos eleitores de Paulo e Márcia na quinzena x são, respectivamente,

em que 0 ≤ x ≤ 36 representa a quinzena, P(x) e M(x) são dados em porcentagens.
De acordo com as pesquisas realizadas, a ordem de preferência nas intenções de voto em Paulo e Márcia sofreram alterações na quinzena
A) 6.
B) 12.
C) 20.
D) 22.
E) 30.
ENADE 2011 - QUESTÃO 17
Considere a função f : R ➝ R definida por y = f(x) = x - 5x² + 4, para cada x ε R. A área da região limitada pelo gráfico da função y = f(x), o eixo Ox e as retas x = 0 e x = 2 é igual a

ENADE 2011 - QUESTÃO 18
Duas grandezas x e y são ditas comensuráveis se existe um número racional q tal que a medida de x é igual a q vezes a medida de y.
Com base nesse conceito, são grandezas comensuráveis
A) a aresta de um cubo de volume V e a aresta de um cubo de volume 2V.
B) a área e o perímetro de um círculo, quando o raio é um número racional.
C) a área e o diâmetro de um círculo, quando o raio é um número racional.
D) o comprimento e o diâmetro de uma circunferência.
E) a diagonal e o lado de um quadrado.
ENADE 2011 - QUESTÃO 19
Sob certas condições, o número de colônias de bactérias, t horas após ser preparada a cultura, é dada pela função

O tempo mínimo necessário para esse número ultrapassar 6 colônias é de
A) 1 hora.
B) 2 horas.
C) 3 horas.
D) 4 horas.
E) 6 horas.
ENADE 2011 - QUESTÃO 20
Considerando a, b e c pertencentes ao conjunto dos números naturais e representando por a|b a relação “a divide b”, analise as proposições abaixo.
I. Se a|(b + c), então a|b ou a|c.
II. Se a|bc e mdc(a,b) = 1, então a|c.
III. Se a não é primo e a|bc, então a|b ou a|c.
IV. Se a|b e mdc(b,c) = 1, então mdc(a,c) = 1.
É correto apenas o que se afirma em
A) I.
B) II.
C) I e III.
D) II e IV.
E) III e IV.
ENADE 2011 - QUESTÃO 21
Os analistas financeiros de uma empresa chegaram a um modelo matemático que permite calcular a arrecadação mensal da empresa ao longo de 24 meses, por meio da função

em que 0 ≤ x ≤ 24 é o tempo, em meses, e a arrecadação A(x) é dada em milhões de reais.
A arrecadação da empresa começou a decrescer e, depois, retomou o crescimento, respectivamente, a partir dos meses
A) x = 0 e x = 11.
B) x = 4 e x = 7.
C) x = 8 e x =16.
D) x = 9 e x =13.
E) x =11 e x = 22.
ENADE 2011 - QUESTÃO 22
Considere u(x, y) = f(x - 4y) + g(x + 4y), em que f e g são funções reais quaisquer, deriváveis até a segunda ordem, com uxx ≠ 0 para todo x e y. Nesse caso,  é igual a
é igual a
 é igual a
é igual aA) - 16.
B) - 8.
C) 0.
D) 8.
E) 16.
ENADE 2011 - QUESTÃO 23
Catedral Metropolitana de Brasília
A construção da Catedral, projeto do arquiteto Oscar Niemeyer, teve início em 12 de agosto de 1958, em plena construção da nova capital. Em 1959, mesmo antes da inauguração de Brasília (1960), a sua forma estrutural (pilares de concreto armado, na forma de um hiperbolóide de revolução) já estava pronta. O fechamento lateral entre os pilares só ocorreu em 1967, pouco antes de sua consagração, em 12 de outubro do mesmo ano, ocasião em que recebeu a imagem de Nossa Senhora Aparecida. De 1969 a 1970, o complexo foi concluído com o espelho d’água ao redor da Catedral, o batistério e o campanário.
PORTO, C. E. Um estudo comparativo da forma estrutural de dois monumentos
religiosos em Brasília: A Catedral e o Estupa Tibetano. Disponível em:
<www.skyscraperlife.com/arquitetura-e-discussoes-urbanas/22122-obrasde-oscar-niemeyer.html>. Acesso em 30 ago. 2011.
Nesse contexto, considere na figura abaixo os elementos principais da hipérbole associada aos arcos hiperbólicos da Catedral Metropolitana de Brasília.
Supondo que o eixo real (ou eixo transverso) da hipérbole na figura II mede 30 m e que a distância focal mede 50 m, analise as seguintes asserções.
Se F1 = (-c, 0) é o foco da hipérbole, então a diretriz associada a ela é a reta d1 : x + 9 = 0.
PORQUE
A equação reduzida dessa hipérbole é 

A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 24
Um instrumento de desenho é constituído de três hastes rígidas AB, AC e BD, articuladas no ponto A, mas fixas em B. A figura a seguir é um esquema desse instrumento, em que as hastes foram substituídas por segmentos de reta.
Na extremidade C, foi colocado um grafite que permite desenhar, sobre uma folha de papel, uma curva γ ao se girar AC em torno de A, mantendo-se fixos AB e BD, que são lados do ângulo α.
Nessa situação, qualquer que seja o ângulo agudo α, a curva γ interceptará a semirreta de origem B e que passa por D em
A) dois pontos E e F distintos, e os triângulos BAE e BAF são congruentes.
B) dois pontos E e F distintos, e os triângulos BAE e BAF são semelhantes, mas não congruentes.

ENADE 2011 - QUESTÃO 25
Considere F : R³ ➝ R uma função diferenciável e suponha F(x, y, z) = 0 que define implicitamente funções não nulas e diferenciáveis z = f(x, y), y - g(x, z) e x = h(y,z).
Nessa situação, analise as afirmações abaixo.
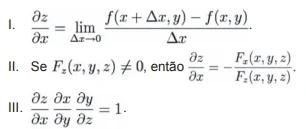
É correto o que se afirma em
A) II, apenas.
B) III, apenas.
C) I e II, apenas.
D) I e III, apenas.
E) I, II e III.
ENADE 2011 - QUESTÃO 26
Na Sociologia da Educação, o currículo é considerado um mecanismo por meio do qual a escola define o plano educativo para a consecução do projeto global de educação de uma sociedade, realizando, assim, sua função social. Considerando o currículo na perspectiva crítica da Educação, avalie as afirmações a seguir.
I. O currículo é um fenômeno escolar que se desdobra em uma prática pedagógica expressa por determinações do contexto da escola.
II. O currículo reflete uma proposta educacional que inclui o estabelecimento da relação entre o ensino e a pesquisa, na perspectiva do desenvolvimento profissional docente.
III. O currículo é uma realidade objetiva que inviabiliza intervenções, uma vez que o conteúdo é condição lógica do ensino.
IV. O currículo é a expressão da harmonia de valores dominantes inerentes ao processo educativo.
É correto apenas o que se afirma em
A) I.
B) II.
C) I e III.
D) II e IV.
E) III e IV.
ENADE 2011 - QUESTÃO 27
O fazer docente pressupõe a realização de um conjunto de operações didáticas coordenadas entre si. São o planejamento, a direção do ensino e da aprendizagem e a avaliação, cada uma delas desdobradas em tarefas ou funções didáticas, mas que convergem para a realização do ensino propriamente dito.
LIBÂNEO, J. C. Didática. São Paulo: Cortez, 2004, p. 72.
Considerando que, para desenvolver cada operação didática inerente ao ato de planejar, executar e avaliar, o professor precisa dominar certos conhecimentos didáticos, avalie quais afirmações abaixo se referem a conhecimentos e domínios esperados do professor.
I. Conhecimento dos conteúdos da disciplina que leciona, bem como capacidade de abordá-los de modo contextualizado.
II. Domínio das técnicas de elaboração de provas objetivas, por se configurarem instrumentos quantitativos precisos e fidedignos.
III. Domínio de diferentes métodos e procedimentos de ensino e capacidade de escolhê-los conforme a natureza dos temas a serem tratados e as características dos estudantes.
IV. Domínio do conteúdo do livro didático adotado, que deve conter todos os conteúdos a serem trabalhados durante o ano letivo.
É correto apenas o que se afirma em
A) I e II.
B) I e III.
C) II e III.
D) II e IV.
E) III e IV.
ENADE 2011 - QUESTÃO 28
Com base na projeção da população brasileira para o período 2010-2040 apresentada nos gráficos, avalie as seguintes asserções.
Constata-se a necessidade de construção, em larga escala, em nível nacional, de escolas especializadas na Educação de Jovens e Adultos, ao longo dos próximos 30 anos.
PORQUE
Haverá, nos próximos 30 anos, aumento populacional na faixa etária de 20 a 60 anos e decréscimo da população com idade entre 0 e 20 anos.
A respeito dessas asserções, assinale a opção correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 29
Na escola em que João é professor, existe um laboratório de informática, que é utilizado para os estudantes trabalharem conteúdos em diferentes disciplinas. Considere que João quer utilizar o laboratório para favorecer o processo ensinoaprendizagem, fazendo uso da abordagem da Pedagogia de Projetos.
Nesse caso, seu planejamento deve
A) ter como eixo temático uma problemática significativa para os estudantes, considerando as possibilidades tecnológicas existentes no laboratório.
B) relacionar os conteúdos previamente instituídos no início do período letivo e os que estão no banco de dados disponível nos computadores do laboratório de informática.
C) definir os conteúdos a serem trabalhados, utilizando a relação dos temas instituídos no Projeto Pedagógico da escola e o banco de dados disponível nos computadores do laboratório.
D) listar os conteúdos que deverão ser ministrados durante o semestre, considerando a sequência apresentada no livro didático e os programas disponíveis nos computadores do laboratório.
E) propor o estudo dos projetos que foram desenvolvidos pelo governo quanto ao uso de laboratórios de informática, relacionando o que consta no livro didático com as tecnologias existentes no laboratório.
ENADE 2011 - QUESTÃO 30
Muitas vezes, os próprios educadores, por incrível que pareça, também vítimas de uma formação alienante, não sabem o porquê daquilo que dão, não sabem o significado daquilo que ensinam e quando interrogados dão respostas evasivas: “é pré-requisito para as séries seguintes”, “cai no vestibular”, “hoje você não entende, mas daqui a dez anos vai entender”.
Muitos alunos acabam acreditando que aquilo que se aprende na escola não é para entender mesmo, que só entenderão quando forem adultos, ou seja, acabam se conformando com o ensino desprovido de sentido.
VASCONCELLOS, C. S. Construção do conhecimento em sala de aula.
13ª ed. São Paulo: Libertad, 2002, p. 27-8.
Correlacionando a tirinha de Mafalda e o texto de Vasconcellos, avalie as afirmações a seguir.
I. O processo de conhecimento deve ser refletido e encaminhado a partir da perspectiva de uma prática social.
II. Saber qual conhecimento deve ser ensinado nas escolas continua sendo uma questão nuclear para o processo pedagógico.
III. O processo de conhecimento deve possibilitar compreender, usufruir e transformar a realidade.
IV. A escola deve ensinar os conteúdos previstos na matriz curricular, mesmo que sejam desprovidos de significado e sentido para professores e alunos.
É correto apenas o que se afirma em
A) I e III.
B) I e IV.
C) II e IV.
D) I, II e III.
E) II, III e IV.
ENADE 2011 - QUESTÃO 31
Ao trabalhar o conteúdo análise combinatória, o professor propôs que os alunos calculassem quantos números distintos de três algarismos podem ser formados a partir de quatro algarismos escolhidos por eles. A seguir, são destacadas as escolhas dos algarismos e as respostas dadas por quatro alunos dessa turma: Ana, Luis, Paulo e Roni.
I. Ana escolheu os algarismos 0, 3, 5 e 7. Sua resposta foi 24, por levar em consideração apenas números com algarismos diferentes entre si.
II. Luis escolheu os algarismos 2, 4, 7 e 8. Sua resposta foi 24, por levar em consideração apenas números com algarismos diferentes entre si.
III. Paulo escolheu os algarismos 3, 4, 5 e 6. Sua resposta foi 16, por levar em consideração a possibilidade de haver algarismos repetidos nos números formados.
IV. Roni escolheu os algarismos 1, 2, 3 e 4. Sua resposta foi 64, por levar em consideração a possibilidade de haver algarismos repetidos nos números formados.
O professor verificou que é coerente com as escolhas e a resposta somente o que se justifica em
A) I.
B) II.
C) I e III.
D) II e IV.
E) III e IV.
ENADE 2011 - QUESTÃO 32
No intuito de proporcionar uma reestruturação dos princípios norteadores da educação nacional, a Lei de Diretrizes e Bases da Educação Nacional (Lei nº 9394/1996) transformou em direito do cidadão e dever do Estado antigos anseios de diversos movimentos populares, entre eles, a oferta de educação escolar regular para jovens e adultos, como se vê no trecho destacado a seguir:
Art. 4º O dever do Estado com educação escolar pública será efetivado mediante a garantia de:
(...)
VII - oferta de educação escolar regular para jovens e adultos, com características e modalidades adequadas às suas necessidades e disponibilidades, garantindose aos que forem trabalhadores as condições de acesso e permanência na escola.
Considerando a modalidade de ensino de que trata esse fragmento da Lei n.º 9394/1996, e para tornar o ensino de matemática mais significativo para quem aprende, o professor deve priorizar
I. atividades que promovam um processo de negociação de significados constituídos com o conteúdo destacado e o sujeito social.
II. atividades que padronizem os procedimentos matemáticos realizados pelos alunos, pois, dessa forma, promoverá o domínio da notação matemática.
III. atividades que, a partir de situações cotidianas, promovam a percepção da relevância do conhecimento matemático.
IV. a linguagem simbólica, pois, dessa forma, poderá promover a percepção das especificidades dessa área de conhecimento.
É correto apenas o que se afirma em
A) I.
B) II.
C) I e III.
D) II e IV.
E) III e IV.
ENADE 2011 - QUESTÃO 33
Para introduzir conceitos relativos a cilindros, um professor de matemática do ensino médio pediu a seus alunos que fizessem uma pesquisa sobre situações práticas que envolvessem essas figuras geométricas. Dois estudantes trouxeram para a sala de aula as seguintes aplicações:
Situação I
O raio hidráulico é um parâmetro importante no dimensionamento de canais, tubos, dutos e outros componentes das obras hidráulicas. Ele é definido como a razão entre a área da seção transversal molhada e o perímetro molhado. Para a seção semicircular de raio r ilustrada abaixo, qual é o valor do raio hidráulico?
Ao analisar as duas situações como possibilidades de recursos didáticos, seria correto o professor concluir que
A) a situação I é inadequada porque induz os estudantes à apreensão equivocada do conceito de cilindro.
B) a situação I é adequada porque permite a discussão de que todas as interseções do cilindro com planos são semicircunferências.
C) a situação II é inadequada porque induz os estudantes à apreensão equivocada do conceito de volume do cilindro.
D) a situação II é adequada porque permite mostrar que o volume do cilindro é igual à quantidade de jabuticabas multiplicada pela média dos volumes das jabuticabas.
E) as situações I e II são adequadas e permitem que sejam explorados os conceitos de seção transversal, área da superfície cilindrica e volume do cilindro.
ENADE 2011 - QUESTÃO 34
No que se refere à organização curricular, avalie as asserções a seguir.
Com relação à organização curricular na área de matemática, as ideias de linearidade e acumulação têm presenças marcantes em diversas produções didáticas da área, pois esse processo linear de trabalho pedagógico é fundamental para a apresentação da conexão e hierarquia das estruturas matemáticas.
PORQUE
Por meio da linearidade, os conteúdos matemáticos são dispostos dos mais simples para os mais complexos, obedecendo a uma estrutura lógica em que cada novo assunto pode ser assimilado pelo aluno, o que propicia o desenvolvimento pleno de sua autonomia acadêmica.
A respeito dessas asserções, assinale a resposta correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 35
Na perspectiva da matemática, de uma forma geral, o jogo é objeto de estudo no campo das probabilidades, enquanto, na perspectiva da pedagogia, é analisado como possibilidade de produção de aprendizagens.
A Educação Matemática propõe análises que permeiam essas duas situações em conjunto, buscando uma interface voltada para a exploração de conceitos e procedimentos matemáticos, análise de dados e interpretação de soluções, por meio de atividades lúdicas em que o desenvolvimento da autonomia do aluno pode ser estimulado. A partir dessas observações, analise as asserções a seguir.
A interface mencionada no texto é possível pois tanto a matemática quanto o jogo se realizam no campo da materialidade.
PORQUE
Sob a perspectiva de atividade matemática, o jogo se encontra no plano epistemológico da matemática que visa abstrair o real, proporcionando um espaço em que o aluno pode, de forma criativa, testar, validar e socializar seus esquemas de ação.
Acerca dessas asserções, assinale a resposta correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 36
Seja A um conjunto e seja ~ uma relação entre pares de elementos de A. Diz-se que ~ é uma relação de equivalência entre pares de elementos de A, se as seguintes propriedades são verificadas, para quaisquer elementos a, a’ e a’’ de A:
(i) a ~ a;
(ii) se a ~ a’, então a’ ~ a;
(iii) se a ~ a’ e a’ ~ a’’, então a ~ a’’.
Uma classe de equivalência do elemento a de A com respeito à relação ~ é o conjunto a = {x ε A : x ~ a}
O conjunto quociente de A pela relação de equivalência ~ é o conjunto de todas as classes de equivalência relativamente à relação ~, definido e denotado como a seguir: A/~ = {a : a ε A}
A função π A ➝ A/~ é chamada projeção canônica e é definida como π (a) = a, ∀a ε A.
Considerando as definições acima, analise as afirmações a seguir.
I. A relação de equivalência ~ no conjunto A particiona o conjunto A em subconjuntos disjuntos, as classes de equivalência.
II. A união das classes de equivalência da relação de equivalência ~ no conjunto A resulta no conjunto das partes de A.
III. Qualquer relação de equivalência no conjunto A é proveniente de sua projeção canônica.
IV. As três relações seguintes são relações de equivalência no conjunto dos números inteiros Z.
É correto apenas o que se afirma em
A) I.
B) II.
C) I e III.
D) II e IV.
E) III e IV
ENADE 2011 - QUESTÃO 37
Para resolver a equação x² = cos x, utiliza-se a fórmula de Taylor da função cos x. Considerando essa observação, analise as afirmações a seguir.
I. As raízes dessa equação, obtidas com uma aproximação de segunda ordem na fórmula de Taylor, são 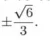
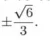
II. O erro de truncamento de uma aproximação de segunda ordem para cos x é limitado por 

III. Ao usar aproximações de quarta ordem em vez de aproximações de segunda ordem para cos x, os erros de truncamento são reduzidos em 25%.
É correto apenas o que se afirma em
A) I.
B) II.
C) III.
D) I e II.
E) II e III.
ENADE 2011 - QUESTÃO 38
O conjunto  , com a operação usual de produto de matrizes, forma um grupo, em que o elemento neutro é a matriz identidade
, com a operação usual de produto de matrizes, forma um grupo, em que o elemento neutro é a matriz identidade 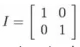 . Dado um elemento A ε G , define-se a ordem de A como sendo o menor inteiro positivo m tal que Am = 1, caso m exista. Se não existir, diz-se que A tem ordem infinita.
. Dado um elemento A ε G , define-se a ordem de A como sendo o menor inteiro positivo m tal que Am = 1, caso m exista. Se não existir, diz-se que A tem ordem infinita.
 , com a operação usual de produto de matrizes, forma um grupo, em que o elemento neutro é a matriz identidade
, com a operação usual de produto de matrizes, forma um grupo, em que o elemento neutro é a matriz identidade 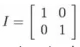 . Dado um elemento A ε G , define-se a ordem de A como sendo o menor inteiro positivo m tal que Am = 1, caso m exista. Se não existir, diz-se que A tem ordem infinita.
. Dado um elemento A ε G , define-se a ordem de A como sendo o menor inteiro positivo m tal que Am = 1, caso m exista. Se não existir, diz-se que A tem ordem infinita.Considerando 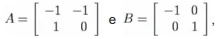 , avalie as asserções a seguir.
, avalie as asserções a seguir.
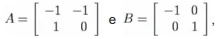 , avalie as asserções a seguir.
, avalie as asserções a seguir.O elemento AB tem ordem seis.
PORQUE
A tem ordem três e B tem ordem dois.
A respeito dessas asserções, assinale a opção correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 39
O gráfico abaixo representa o traço da curva parametrizada diferenciável plana

A respeito dessa curva, avalie as afirmações a seguir.
I. α é injetiva no intervalo (0, 2π).
II. α tem curvatura constante.
III. α(t + 2π) = a(t) para todo t ε R.
IV. α tem vetor tangente unitário em t = 0, com a´(0) = (-1, 0).
V. O traço de α está contido em um círculo de raio r < (e + 2).
É correto apenas o que se afirma em
A) II.
B) I e II.
C) I e IV.
D) III e V.
E) III , IV e V.
ENADE 2011 - QUESTÃO 40
Considerando E um espaço métrico, A ⊂ E um conjunto aberto e (xn) ⊂ E uma sequência convergente para p ∈ A, analise as afirmações abaixo.
I. O complementar de A é fechado em E.
II. Toda vizinhança aberta de p está contida em A.
III. xn ∈ A, para todo n suficientemente grande.
É correto apenas o que se afirma em
A) I.
B) II.
C) III.
D) I e II.
E) I e III.
ENADE 2011 - QUESTÃO 41
Um peso atado a uma mola move-se verticalmente para cima e para baixo de tal modo que a equação do movimento é dada por s´´ (t) + 16s(t) = 0 em que s(t) é a deformação da mola no tempo t.
Sabe-se que s(t) = 2 e s`(t) = 1, para t = 0.
Para a função deformação s(t), tem-se que s(t) = 0 quando t é igual a

ENADE 2011 - QUESTÃO 42
Considere a transformação linear T: IR² → IR² definida por T(x,y) = (2x + 6y, 6x + 2y). Com relação a esse operador, analise as asserções a seguir.
O núcleo de T é um subespaço vetorial de IR² de dimensão 1.
PORQUE
T é um operador normal.
A respeito dessas asserções, assinale a opção correta.
A) As duas asserções são proposições verdadeiras, e a segunda é uma justificativa correta da primeira.
B) As duas asserções são proposições verdadeiras, mas a segunda não é uma justificativa correta da primeira.
C) A primeira asserção é uma proposição verdadeira, e a segunda, uma proposição falsa.
D) A primeira asserção é uma proposição falsa, e a segunda, uma proposição verdadeira.
E) Tanto a primeira quanto a segunda asserções são proposições falsas.
ENADE 2011 - QUESTÃO 43
Considerando  campo elétrico criado por uma carga q localizada na origem, analise as afirmações abaixo.
campo elétrico criado por uma carga q localizada na origem, analise as afirmações abaixo.
 campo elétrico criado por uma carga q localizada na origem, analise as afirmações abaixo.
campo elétrico criado por uma carga q localizada na origem, analise as afirmações abaixo.I. O campo elétrico criado pela carga q é de classe C¹ em IR³.
II. Independe do raio da superfície esférica o fluxo do campo E através de uma superfície esférica de raio r, centrada na origem, cuja normal n aponta para fora da esfera.
III. É sempre um número maior que 4 o fluxo do campo E através de uma superfície esférica de raio r, centrada na origem, cuja normal aponta n para fora da esfera.
É correto o que se afirma em
A) II, apenas.
B) III, apenas.
C) I e II, apenas.
D) I e III, apenas.
E) I, II e III.
ENADE 2011 - QUESTÃO 44
Um dos problemas mais antigos da Matemática é encontrar raízes de equações polinomiais. Quando se fala de variáveis complexas, sabe-se que toda equação polinomial de grau n possui exatamente n zeros. No entanto, um problema que surge nesse ponto é que nem sempre conseguimos dizer quem são essas n raízes. Como corolário do Princípio do Argumento, um dos principais resultados da Análise Complexa e particularmente da Teoria dos Resíduos, temse o Teorema de Rouché, que possibilita, em algumas situações, localizar os zeros de equações polinomiais. Segue abaixo o enunciado desse teorema.
Considere f e g funções que são meromorfas (holomorfas a menos de um conjunto discreto de polos) em um subconjunto não vazio, aberto e conexo UC do conjunto dos números complexos e γ : I ➝ C uma curva fechada simples (sem autointerseções), cujo interior R esteja contido em U. Se γ(I) não contém polos de f e nem zeros de g e |f(z)| > |g(z)| para todo z ε γ(I), então Z(f + g,R) - P(f + g, R) = Z( f, R) - P(f,R)
em que Z(h, A) e P(h, A) denotam, respectivamente, o número de zeros e o número de polos de uma função h em A.
Considerando o teorema acima e a equação z - 2z³ + 5 = 0, conclui-se que existem raízes dessa equação que satisfazem à condição

ENADE 2011 - QUESTÃO 45
A aplicação φ S1 → S2 ilustrada na figura abaixo é uma isometria entre a faixa plana S1 e o cilindro circular reto S2. A isometria leva o segmento de reta r1 em um arco de circunferência em S2 e o segmento de reta r2 em um segmento de reta de S2.
Nessa situação, a imagem do segmento de reta r3 pela isometria φ é uma
A) espiral da superfície S2.
B) curva plana contida em S2.
C) geodésica da superfície S2.
D) linha assintótica da superfície S2.
E) linha de curvatura da superfície S2.

















COMENTÁRIOS