Prova ENADE 2021 Matemática (licenciatura) com Gabarito

Prova ENADE 2021 Matemática (licenciatura) com Gabarito

Prova ENADE 2021 Matemática (licenciatura) com Gabarito

OBS: As questões objetivas de 01 a 08 estão disponível na prova de Formação Geral que você pode acessar clicando neste link ou neste link e/ou neste link. As questões discursivas não foram disponibilizadas com padrão de resposta. Assim que divulgadas serão atualizadas.

CONHECIMENTO ESPECÍFICO

ENADE 2021 - QUESTÃO DISCURSIVA 03

A Base Nacional Comum Curricular (BNCC), para o Ensino Médio, contempla a habilidade “de construir e interpretar tabelas e gráficos de frequências com base em dados obtidos em pesquisas por amostras estatísticas, incluindo ou não o uso de softwares que inter-relacionem estatística, geometria e álgebra, no eixo de estatística e probabilidade.”

BRASIL. Ministério da Educação. Secretaria de Educação Básica.

Base Nacional Comum Curricular (BNCC). Brasília, 2018 (adaptado).

A fim de desenvolver em seus alunos a habilidade descrita na BNCC, um professor de Matemática optou por fazer uso de um software de geometria dinâmica que reúne recursos de geometria, álgebra, cálculo e estatística.

Considerando a habilidade curricular a ser desenvolvida e o recurso tecnológico mencionado, discorra sobre duas vantagens e duas desvantagens do uso dessa estratégia didática pelo professor. (valor: 10,0 pontos)

PADRÃO DE RESPOSTA. (EM BREVE)

ENADE 2021 - QUESTÃO DISCURSIVA 04

Uma sequência de números reais é uma função x : N → R, que associa a cada número natural n um número real xn, chamado o n -ésimo termo da sequência.

Dizemos que uma sequência (xn) n ∈ N de números reais converge para o número real L se, dado ∈ > 0, existe n0 tal que n > n0 implica |xn - L| < ∈, e escrevemos 

Dada uma sequência x = (xn) n ∈ N de números reais, uma subsequência de x é a restrição da função x a um subconjunto infinito N ⊂ N.

Pode-se estabelecer, ainda, muitos resultados sobre convergência de sequências e subsequências.

Considerando as informações e a sequência apresentadas, faça o que se pede nos itens a seguir.

a) Mostre que  se, e somente se, (valor: 6,0 pontos)

b) Dê exemplo de uma sequência (xn) n ∈ N tal que exista    mas não exista  (valor: 4,0 pontos)

PADRÃO DE RESPOSTA. (EM BREVE)

ENADE 2021 - QUESTÃO DISCURSIVA 05

TEXTO I

Os Parâmetros Curriculares Nacionais (PCN) explicitam o papel da Matemática no Ensino Fundamental pela proposição de objetivos que evidenciam a importância de o aluno valorizá-la como instrumental para compreender o mundo à sua volta. Além disso, destacam que essa área do conhecimento é fruto da criação e da invenção humana, seguindo caminhos diferentes nas diversas culturas.

BRASIL. Ministério da Educação. Secretaria de Educação

Fundamental. Parâmetros Curriculares Nacionais:

Matemática. Brasília, 1998 (adaptado).

TEXTO II

A Base Nacional Comum Curricular (BNCC) aprofunda e amplia alguns dos objetivos dos Parâmetros Curriculares Nacionais (PCN), destacando que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo. Nas competências específicas da Matemática para o Ensino Fundamental, é ressaltado o reconhecimento desse componente curricular como uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos – uma ciência viva que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

BRASIL. Ministério da Educação. Secretaria de Educação Básica.

Base Nacional Comum Curricular (BNCC). Brasília, 2018 (adaptado).

Considerando as ideias sobre a Matemática abordadas nos textos apresentados, faça o que se pede nos itens a seguir.

a) Comente como um professor de Educação Básica pode abordar, nas aulas de Matemática, a evolução dessa ciência. (valor: 4,0 pontos)

b) Explique como a produção do conhecimento matemático se sucede ao longo do tempo. (valor: 3,0 pontos)

c) Discorra sobre uma das contribuições de algumas civilizações e culturas antigas na construção do conhecimento matemático usado na atualidade. (valor: 3,0 pontos)

PADRÃO DE RESPOSTA. (EM BREVE)

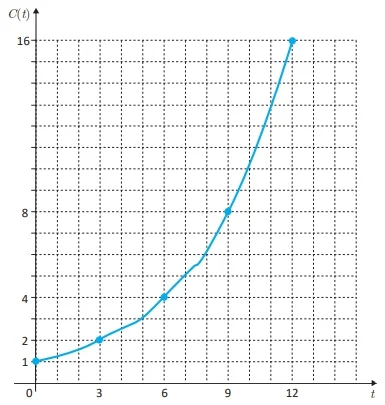
ENADE 2021 - QUESTÃO 09

Com o agravamento da pandemia do novo Coronavírus (Sars-CoV-2), alguns termos tornaram-se mais conhecidos, dentre eles o de crescimento exponencial.

O gráfico da função exponencial a seguir representa a evolução do crescimento do número de pessoas contaminadas por uma doença ao longo do tempo, medido em dias. Observe que o número de pessoas contaminadas dobra a cada três dias.

Supondo que a tendência de crescimento do número de pessoas contaminadas apresentada no gráfico se mantenha ao longo do tempo e seja exponencial, avalie as afirmações a seguir.

I. Se C(t) representa o número de pessoas contaminadas no tempo t, então

II. A velocidade de crescimento da contaminação no nono dia é  pessoas/dia.

III. Com um mês de epidemia, o número de contaminados ultrapassa o de 1 000 pessoas.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 10

Anualmente é realizado no Brasil o Censo da Educação Superior, que coleta e reúne informações dos cursos de graduação das diversas instituições de Ensino Superior. No Censo de 2017, foram apresentados dados da distribuição de alunos matriculados em cursos de licenciatura.

Os gráficos a seguir apresentam informações do percentual de alunos em relação ao sexo, à organização acadêmica, à categoria administrativa e à modalidade de ensino.

Distribuição dos alunos matriculados em cursos de graduação em licenciatura - 2017

Disponível em: http://portal.mec.gov.br. Acesso em: 21 de maio 2020.

Considerando as informações apresentadas nos gráficos, assinale a opção correta.

A) A maior quantidade de alunos matriculados é do sexo feminino e está na rede pública de ensino.

B) A rede pública possui a maior quantidade de alunos matriculados na modalidade de ensino a distância e a maior parte é do sexo masculino.

C) A organização universidade possui a menor quantidade de alunos matriculados e a menor parte é do sexo feminino.

D) A modalidade de ensino a distância tem a menor quantidade de alunos matriculados em relação à modalidade presencial.

E) A menor quantidade de alunos matriculados é do sexo masculino, da rede pública e na modalidade presencial.

GABARITO.

ENADE 2021 - QUESTÃO 11

Uma elipse é o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante.

Considere a ilustração da elipse.

A equação reduzida dessa elipse é 

Com base nas informações apresentadas, avalie as afirmações a seguir.

I. -a ≤ x ≤ a e -b ≤ y ≤ b.

II. A elipse está contida em uma circunferência de raio b.

III. Se (x,y) é solução da equação reduzida, então (-x,-y), (x,-y) e (-x,y) também satisfazem a equação da elipse.

IV. Uma outra forma de representar a elipse dada é b²x² + a²y² - ² = 0.

É correto apenas o que se afirma em

A) I e III.

B) II e III.

C) II e IV.

D) I, II e IV.

E) I, III e IV.

GABARITO.

ENADE 2021 - QUESTÃO 12

No início do semestre letivo, um estudante tomou emprestado da biblioteca 7 livros, sendo 4 de Geometria, 1 de Topologia e 2 de Álgebra. Chegando em casa, ele os dispôs aleatoriamente em uma prateleira da estante. No dia seguinte, para facilitar a consulta a esse material, o aluno decidiu organizar os livros de forma que o de Topologia separasse os de Geometria dos de Álgebra, não importando qual agrupamento ficasse à direita ou à esquerda. Ao chegar à estante, percebeu, curiosamente, que a disposição dos livros atendia àquilo que ele havia planejado. Pelos seus cálculos, a quantidade de diferentes disposições dos 7 livros na prateleira seria de 7!, que resulta em 5 040 possibilidades.

Qual a probabilidade de os livros terem sido dispostos da forma que o estudante decidiu organizá-los?

GABARITO.

ENADE 2021 - QUESTÃO 13

O teorema do valor médio afirma que, se uma função f é definida e contínua em um intervalo fechado [a, b], sendo derivável no intervalo aberto (a, b), existe um ponto c em (a, b) tal que

Considerando esse contexto, avalie as asserções a seguir e a relação proposta entre elas.

I. Existe um ponto c no intervalo aberto (a, b) tal que a reta tangente ao gráfico de f neste ponto é paralela à reta secante que passa pelos extremos do gráfico de f restrita ao intervalo fechado [a, b].

PORQUE

II. Se uma função é derivável em um certo ponto, a reta tangente ao gráfico da função nesse ponto pode ser obtida como o limite de uma sequência de retas secantes.

A respeito dessas asserções, assinale a opção correta.

A) As asserções I e II são proposições verdadeiras, e a II é uma justificativa correta da I.

B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.

C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.

D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.

E) As asserções I e II são proposições falsas.

GABARITO.

ENADE 2021 - QUESTÃO 14

Para demonstrar a importância do uso de novas tecnologias na Educação Básica, uma professora de Matemática propôs o problema a seguir, que envolve medidas estatísticas de um conjunto de dados. Uma loja vende quatro tipos de bicicletas com os seguintes preços por unidade: a bicicleta da marca A custa R$150,00; a da marca B, R$250,00; a da marca C, R$300,00; e a da marca D, R$400,00. Em uma semana, foram vendidas 11 bicicletas na seguinte ordem de marcas: A, D, D, D, B, D, B, D, B, B e A.

Utilizando um software estatístico, a professora mostrou que é possível encontrar a média, a mediana e a moda do conjunto dos valores das vendas das bicicletas (obtidos na mesma ordem de venda).

Considerando a situação apresentada, avalie as afirmações a seguir.

I. A média do conjunto dos valores das vendas das bicicletas é igual ao valor de uma bicicleta da marca C.

II. A mediana e a moda do conjunto dos valores das vendas das bicicletas são iguais.

III. A mediana do conjunto dos valores das vendas das bicicletas é maior que a média desses valores.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 15

Considerando que, dados os inteiros m e n, o mdc (m, n) é o maior divisor comum, e o mmc (m, n) é o menor múltiplo comum de m e n, avalie as afirmações a seguir.

I. O resto da divisão de 7 ´ 18 - 2 por 7 é 5.

II. Se m = 7 ´ 22 + 5 e n = 7 ´ 38 + 6, o resto da divisão de m + n por 7 é 3.

III. O mmc (m, n) é um divisor do mdc (m, n).

IV. mdc (m, n) ´ mmc (m, n) = m ´ n.

É correto apenas o que se afirma em

A) I e III.

B) I e IV.

C) II e III.

D) I, II e IV.

E) II, III e IV.

GABARITO.

ENADE 2021 - QUESTÃO 16

A modalidade de Ensino a Distância (EaD) está cada vez mais presente na sociedade, principalmente nos cursos de licenciatura de diversas áreas; por exemplo, no de licenciatura em Matemática. Na atualidade, os avanços das tecnologias da informação e comunicação (TIC) oferecem diferentes possibilidades e desafios, além de novas concepções e práticas de avaliação.

Acredita-se ser essencial que a avaliação da aprendizagem na modalidade a distância se caracterize como um processo contínuo e formativo, possibilitando não só o acompanhamento da aprendizagem discente, mas também o desenvolvimento da autonomia crítica do aluno. E o EaD, com diferentes recursos e meios, pode estimular a aprendizagem do estudante no processo de ensino dos conteúdos matemáticos.

Disponível em: http://www.ucs.br. Acesso em: 6 jun. 2020 (adaptado).

A partir do tema tratado no texto, avalie as afirmações a seguir.

I. Dado que a avaliação é um processo contínuo e formativo, no qual devam ser considerados vários aspectos e condições de ensino dos conteúdos matemáticos, as características próprias do EaD precisam ser levadas em conta no processo de avaliação da aprendizagem dos alunos.

II. A modalidade de EaD tem características próprias de ensino que devem ser consideradas na avaliação dos alunos, por isso, deve privilegiar o processo formativo no ensino e aprendizagem dos conteúdos matemáticos.

III. Os avanços das TIC oferecem diversas possibilidades de ensino dos conteúdos matemáticos, por isso, a modalidade de EaD deve utilizar os inúmeros recursos tecnológicos disponíveis para favorecer a aprendizagem dos alunos e criar novas formas de avaliação.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 17

A Base Nacional Comum Curricular (BNCC), área da Matemática, Ensino Fundamental, contempla o desenvolvimento da compreensão de conceitos e procedimentos em seus diferentes campos, visando à resolução de situações-problema. No Ensino Médio, na área de Matemática e suas Tecnologias, os estudantes devem utilizar conceitos, procedimentos e estratégias não apenas para resolver problemas, mas também para formulá-los, descrever dados, selecionar modelos matemáticos e desenvolver o pensamento computacional, por meio da utilização de diferentes recursos da área.

BRASIL. Ministério da Educação. Secretaria de Educação Básica. 

Base Nacional Comum Curricular (BNCC). Brasília, 2018 (adaptado).

Acerca do que propõe a BNCC para o desenvolvimento do pensamento computacional no ensino da Matemática, avalie as asserções a seguir e a relação proposta entre elas.

I. O jogo “Travessia” – na versão do lobo, da ovelha e da couve, na qual o barqueiro necessita atravessar um deles de cada vez de uma margem para outra de um rio, sabendo que o lobo não pode ficar sozinho com a ovelha e que a ovelha não pode ficar sozinha com a couve – pode ser utilizado para desenvolver o pensamento computacional no ensino da Matemática.

PORQUE

II. O pensamento computacional parte geralmente de situações-problema, por meio das quais se busca desenvolver procedimentos e estratégias como também levantar dados para elaborar hipóteses e utilizar possíveis modelos matemáticos na solução do problema, tomando-se por base o procedimento algorítmico.

A respeito dessas asserções, assinale a opção correta.

A) As asserções I e II são proposições verdadeiras, a II é uma justificativa correta da I.

B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.

C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.

D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.

E) As asserções I e II são proposições falsas.

GABARITO.

ENADE 2021 - QUESTÃO 18

A teoria da probabilidade nasceu das discussões matemáticas que aconteciam, por correspondência, entre Pascal e Pierre de Fermat. Antes disso, esse ramo da matemática era trabalhado de forma apenas intuitiva e empregado principalmente na resolução de problemas que uniam matemática e jogos. A partir da origem dessa teoria, outros matemáticos deram valiosas contribuições para o seu desenvolvimento, cujas aplicações atualmente podem ser encontradas em Estatística, em Biologia, em Psicologia e em várias outras áreas.

BOYER, C. B. História da Matemática. São Paulo: 

Edgard Blücher/Edusp, 1974 (adaptado).A partir das informações do texto, avalie as afirmações a seguir, acerca da evolução histórica do conhecimento matemático.

I. A matemática é uma construção humana em que os conceitos têm sido desenvolvidos para resolver problemas relacionados às necessidades de diversas culturas, em seus diferentes momentos históricos.

II. As soluções de problemas de diversas naturezas foram se constituindo em teorias, por meio de questionamentos, respostas e novas problematizações, fazendo emergir o conhecimento matemático.

III. As percepções que os matemáticos têm do próprio objeto matemático são imutáveis ao longo do tempo, embora a elas se somem contribuições de estudiosos de diferentes áreas.

É correto o que se afirma em

A) I, apenas.

B) III, apenas.

C) I e II, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 19

Arthur (1), Bruno (2), Guilherme (3) e Matheus (4) são irmãos que gostam de jogar videogame e de se desafiarem nos jogos.

Considerando a matriz A = (aij) 4 x 4, em que cada elemento aij representa o número de desafios que o irmão i fez ao irmão j:

a diferença entre o número de desafios propostos pelo irmão que mais desafiou e o número de desafios recebidos pelo irmão que menos foi desafiado é igual a

A) 0.

B) 1.

C) 2.

D) 10.

E) 14.

GABARITO.

ENADE 2021 - QUESTÃO 20

A equação  corresponde a um modelo de uma aplicação bancária com capitalização contínua, em que S é o saldo dessa aplicação em um instante t, r é a taxa de juros, constante, dessa aplicação bancária, e k representa os depósitos (k>0) e as retiradas (k<0).

Com base nas informações apresentadas, avalie as afirmações a seguir.

I. O modelo matemático que representa esse sistema de capitalização é uma equação diferencial linear de primeira ordem.

II. Essa equação é insolúvel, pois os valores de r e de k são desconhecidos.

III. Se não houver depósitos nem retiradas, k=0, então o saldo bancário pode ser expresso por

onde S0 é o capital inicialmente investido.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 21

A atividade de jogar, se bem orientada, tem papel importante no desenvolvimento de habilidades de raciocínio, como organização, atenção e concentração, tão necessárias para o aprendizado, em especial da Matemática, e para a resolução de problemas em geral. Também no jogo, identificamos o desenvolvimento da linguagem, da criatividade e do raciocínio dedutivo, exigidos na escolha de uma jogada e na argumentação necessária durante a troca de informações.

BORIN, J. Jogos e resolução de problemas: uma estratégia

para as aulas de matemática. São Paulo: IME-USP, 2004 (adaptado).

A partir do tema tratado no texto, avalie as afirmações a seguir.

I. Uma metodologia de ensino que faz uso de jogos pode desenvolver a capacidade do aluno para entender e, até mesmo, justificar afirmações matemáticas.

II. O êxito das metodologias que utilizam resolução de problemas, de maneira geral, depende dos jogos.

III. Os jogos eletrônicos, atualmente, são as melhores opções para se desenvolver a capacidade intelectual dos estudantes.

IV. A capacidade de organizar e expressar ideias e o aumento de concentração são algumas das habilidades proporcionadas pelos jogos.

É correto apenas o que se afirma em

A) I e II.

B) I e IV.

C) II e III.

D) I, III e IV.

E) II, III e IV.

GABARITO.

ENADE 2021 - QUESTÃO 22

O Salto de Rã é um jogo composto por um número ímpar de casas e um número par de peças. O objetivo do jogo é trocar as peças de lugar utilizando o mínimo possível de movimentos. No caso, as peças que estão no lado direito devem ser colocadas no lado esquerdo e vice-versa. O jogador só pode fazer um movimento por vez, e só é permitido saltar uma peça.

A figura a seguir ilustra essa situação.

O jogo pode ser utilizado em níveis diferentes de ensino, trabalhando conceitos de contagem e de sequência. Na formação das jogadas, pode-se, a partir dos movimentos obtidos, preencher tabelas com valores numéricos que possibilitam determinar a função discreta y = 2n + n², que representa o número mínimo de movimentos em relação ao número de peças.

MENEZES, J. E. (org.). Conhecimento, interdisciplinaridade e

atividades de ensino com jogos matemáticos: uma proposta metodológica. 

Série Contexto Matemático, v. 5. UFRPE, Recife, 2008 (adaptado).

Em qual das opções a seguir se representa o esboço do gráfico de y = 2n + n²?

GABARITO.

ENADE 2021 - QUESTÃO 23

Para se chegar à resolução de alguns problemas geométricos, pode haver mais de um caminho; por exemplo, quando se pede que, dado um triângulo equilátero ABC, seja determinado um ponto P, no interior ou sobre os lados do triângulo, de tal modo que a soma das distâncias de P a cada um dos três lados seja mínima. A resposta desse problema é interessante, pois qualquer que seja a posição do ponto P, a soma das distâncias a cada lado do triângulo é sempre a mesma: a altura do triângulo, nesse caso. Para resolver esse problema, pode-se utilizar a geometria analítica ou as transformações geométricas.

VELOSO, E. Geometria: temas actuais. Material para professores.

Instituto de Educação Educacional, Lisboa, 1998 (adaptado).

Com base no texto apresentado, avalie as informações a seguir.

I. A utilização da resolução de problemas geométricos nas aulas de Matemática permite que o professor aborde situações em diversos contextos e, ao mesmo tempo, trabalhe, de forma didática com os alunos, o rigor e a formalidade matemáticos.

II. A resolução de problemas geométricos nas aulas de Matemática, para que seja válida, exige do aluno rigor e formalidade, além da necessidade de apresentar mais de um caminho para a resposta.

III. O professor, ao utilizar o problema geométrico citado, na aula de Matemática, deve explicar a resolução com rigor e formalidade, para que os alunos abstraiam e memorizem o raciocínio empregado e passem a adotá-lo daí em diante, na solução dos demais problemas matemáticos.

É correto o que se afirma em

A) I, apenas.

B) III, apenas.

C) I e II, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 24

As Tendências em Educação Matemática, presentes nos cursos de licenciatura em Matemática, complementam o processo de formação dos futuros professores e proporcionam o estudo dos meios de ensino que possam ser aplicados para desenvolver as competências previstas na Educação Básica. A Base Nacional Comum Curricular (BNCC), área de Matemática e suas tecnologias, Ensino Médio, orienta que, para o desenvolvimento de competências que envolvem o raciocinar, é necessário que os estudantes possam, em interação com seus colegas e professores, investigar, explicar e justificar os problemas resolvidos, com ênfase nos processos de argumentação matemática. Embora todas as habilidades pressuponham a mobilização do raciocínio, nem todas se restringem ao seu desenvolvimento. Assim, por exemplo, a identificação de regularidades e padrões exige, além de raciocínio, a representação e a comunicação para expressar as generalizações, bem como a construção de uma argumentação consistente para justificar o raciocínio utilizado.

BRASIL. Ministério da Educação. Secretaria de Educação Básica. Base Nacional Comum Curricular (BNCC). Brasília, 2018 (adaptado).

Acerca das Tendências em Educação Matemática e do que propõe a BNCC para o desenvolvimento de competências que envolvem o raciocinar no ensino da Matemática, avalie as asserções a seguir e a relação proposta entre elas.

I. A Resolução de Problemas Matemáticos, a Modelagem Matemática, a Etnomatemática e a História da Matemática são consideradas Tendências em Educação Matemática que possibilitam ao professor explorar outras propostas de ensino dos conceitos matemáticos.

PORQUE

II. O desenvolvimento de competências para o raciocínio é importante para estruturar as respostas e explicações dos alunos ao se depararem com a resolução de problemas matemáticos, desenvolvendo estratégias de investigação e de argumentação.

A respeito dessas asserções, assinale a opção correta.

A) As asserções I e II são proposições verdadeiras, a II é uma justificativa correta da I.

B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.

C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.

D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.

E) As asserções I e II são proposições falsas.

GABARITO.

ENADE 2021 - QUESTÃO 25

No Brasil, cerca de 90% das pessoas com mais de 25 anos não poupam dinheiro pensando na aposentadoria, segundo pesquisa feita com base na avaliação da estrutura previdenciária de 70 países. Em locais como Nova Zelândia e Estados Unidos, esse percentual é de cerca de 30% e 40%, respectivamente. Mesmo países emergentes, como a Índia e Rússia, têm percentuais melhores que o brasileiro, algo em torno de 80%. Mas também existem países em situações ainda piores, como Argentina e Egito, onde cerca de 95% da população nessa faixa etária não guarda dinheiro para o futuro.

Disponível em: https://www.infomoney.com.br 

Acesso em: 28 jun. 2020 (adaptado).

Ao se analisar a qualidade final dos sistemas previdenciários, pode-se observar a situação de alguns países e a posição do Brasil neste ranking, como demonstra a representação gráfica a seguir.

Obs.: As notas vão de 1 a 7, sendo 1 a melhor nota.

Disponível em: https://www.infomoney.com.br.

Acesso em: 28 jun. 2020 (adaptado).

Com base no contexto e na representação gráfica apresentados, é correto afirmar que

A) o Brasil apresenta 3,98% da população investindo no sistema previdenciário.

B) os países com nota máxima 1 e mínima 7 não foram apresentados neste ranking.

C) a Suécia tem a menor nota, sendo, portanto, o país que apresenta o pior sistema previdenciário do mundo.

D) o Brasil, dos 70 países participantes da pesquisa, está entre aqueles que apresentam os 10 melhores sistemas previdenciários do mundo.

E) o índice dos 5 países com os melhores sistemas previdenciários do mundo está, no mínimo, a 0,94 pontos do Brasil.

GABARITO.

ENADE 2021 - QUESTÃO 26

TEXTO I

É cada dia mais presente a integração das tecnologias digitais na educação. Essa integração propicia que parte do ensino seja presencial e parte virtual (ensino híbrido), dando liberdade ao aluno para gerenciar seus horários de estudo. O ensino híbrido é um modelo de educação formal que se caracteriza por mesclar dois modos de ensino; o online e o presencial. Nesse ensino, é fundamental a utilização de novas metodologias que promovam a autonomia do estudante.

Disponível em: http://www.pos.cps.sp.gov.br.

Acesso em: 27 jun. 2020 (adaptado).

TEXTO II

As metodologias ativas são caminhos para avançar mais no conhecimento profundo, nas competências socioemocionais e em novas práticas. Se queremos que os alunos sejam proativos, precisamos adotar metodologias em que eles se envolvam em atividades cada vez mais complexas, em que tenham que tomar decisões e avaliar os resultados, com apoio de materiais relevantes.

Disponível em: http://www2.eca.usp.br. Acesso em: 27 jun. 2020 (adaptado).

Com base nos textos I e II, avalie as afirmações a seguir.

I. No ensino presencial e online, o material didático, além de motivar o aluno, deve propiciar o desenvolvimento da autonomia e a construção do conhecimento.

II. Dada a característica abstrata da disciplina de matemática, os materiais didáticos assumem um papel preponderante nas aulas, e a sua utilização determina a aprendizagem do aluno.

III. O material didático construído para o ensino online por meio de abordagem que privilegie a capacidade de reflexão do aluno permite propiciar uma mediação pedagógica voltada para a construção do conhecimento.

É correto o que se afirma em

A) I, apenas. 

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 27

Buscando levar o aluno a construir ou ampliar o conhecimento sobre equações de primeiro grau, o professor propôs o seguinte problema.

Um colar se rompeu quando duas amigas brincavam.

Uma fileira de pérola escapou.

A sexta parte das pérolas ao solo caiu.

Um terço das pérolas uma jovem salvou.

A décima parte a outra jovem salvou.

E com seis pérolas o colar ficou.

Diga-me, quantas pérolas tinha a fileira que escapou?

GUSMÃO, G. A. P. et al. (ed.). VII Olimpíada de Matemática do 

Estado de Goiás: resolução comentada das provas. 

Goiânia: UFG, 1999 (adaptado).

Depois de um tempo, um dos alunos afirmou:

“professor, esse problema está mal elaborado!”

Após análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas.

I. O aluno está certo, a única solução possível para esse problema é incoerente com o enunciado.

PORQUE

II. A quantidade de pérolas deve ser divisível por 3, por 6 e por 10.

A respeito dessas asserções assinale a opção correta.

A) As asserções I e II são proposições verdadeiras, e a II é uma justificativa correta da I.

B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.

C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.

D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.

E) As asserções I e II são falsas.

GABARITO.

ENADE 2021 - QUESTÃO 28

A figura mostra um cubo ABCDEFGH de aresta 4.

Seja P um ponto sobre o segmento FH, suponha que o ângulo  mede 30°.

Nessas condições, avalie as seguintes afirmações.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 29

Etnomatemática não é apenas o estudo de “matemáticas das diversas etnias”. Criei essa palavra para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).

A disciplina denominada Matemática é, na verdade, uma etnomatemática que se originou e se desenvolveu na Europa mediterrânea, tendo recebido algumas contribuições das civilizações indiana e islâmica, e que chegou à forma atual nos séculos XVI e XVII, sendo, a partir de então, levada e imposta a todo o mundo.

Hoje, essa matemática adquire um caráter de universalidade, sobretudo devido ao predomínio da ciência e tecnologia modernas, que foram desenvolvidas a partir do século XVII na Europa. Essa universalização é um exemplo do processo de globalização que estamos testemunhando em todas as atividades e áreas de conhecimento.

D’AMBROSIO, Ubiratan. Sociedade, cultura, matemática e seu ensino.

Educação e Pesquisa, São Paulo, v. 31, n. 1, p. 99-120, jan./abr. 2005 (adaptado).

A reflexão que o texto promove vai ao encontro do comprometimento docente com a prática pedagógica de modo a acompanhar a evolução do conhecimento matemático. A partir dessa perspectiva, avalie as afirmações a seguir.

I. O recurso à história da matemática serve de contexto para introduzir e problematizar ideias matemáticas.

II. O currículo para o ensino de matemática deve se articular com diferentes áreas para possibilitar o desenvolvimento do pensamento analítico.

III. O professor precisa valorizar a utilização de diferentes e novas tecnologias na sala de aula com a finalidade de verificar principalmente as competências individuais do aluno.

É correto o que se afirma em

A) I, apenas.

B) III, apenas.

C) I e II, apenas.

D) II e III, apenas.

E) I, II e III.

GABARITO.

ENADE 2021 - QUESTÃO 30

Seja T : R² → R² a transformação linear dada pela reflexão em torno do eixo x, seguida da rotação de 90° no sentido anti-horário e da dilatação de fator 2.

Com base nessas informações, é correto afirmar que T(20, 24) é igual a

A) (40, 48).

B) (48, 40).

C) (40, -48).

D) (48, -40).

E) (-48, -40).

GABARITO.

ENADE 2021 - QUESTÃO 31 - LICENCIATURA

Os quilombolas, compreendidos também como povos ou comunidades tradicionais, exigem que as políticas públicas a eles destinadas considerem a sua inter-relação com as dimensões históricas, políticas, econômicas, sociais, culturais e educacionais que acompanham a constituição dos quilombos no Brasil. Consequentemente, a Educação Escolar Quilombola não pode ser pensada somente se levando em conta os aspectos normativos, burocráticos e institucionais relacionados à configuração das políticas educacionais. A sua implementação deverá ser sempre acompanhada de consulta prévia e realizada pelo poder público junto às comunidades quilombolas e suas organizações.

BRASIL/CNE. Parecer CNE/CEB n. 16/2012. Diretrizes Curriculares 

Nacionais para a Educação Escolar Quilombola, 2012 (adaptado).

Considerando o texto e as discussões sobre políticas de articulação escola/comunidade quilombola, avalie as afirmações a seguir.

I. A relação entre educação e movimentos sociais na educação quilombola objetiva adequar essa organização cultural ao sistema educacional.

II. A história, a memória, o território, a ancestralidade e os conhecimentos tradicionais da comunidade quilombola são aspectos considerados na garanti a do direito à educação quilombola.

III. O papel da comunidade quilombola é determinante nos processos decisórios acerca da educação escolar a ser nela implementada.

É correto o que se afirma em

A) I, apenas.

B) II, apenas.

C) I e III, apenas.

D) II e III, apenas.

E) I, II e III. 

GABARITO.

ENADE 2021 - QUESTÃO 32 - LICENCIATURA

O pensamento de Paulo Freire – a sua teoria do conhecimento – deve ser entendido no contexto em que surgiu o Nordeste brasileiro, onde, no início da década de 1960, metade de seus 30 milhões de habitantes vivia na “cultura do silêncio”, como ele dizia, isto é, eram analfabetos. Era preciso “dar-lhes a palavra” para que transitassem para a participação na construção de um Brasil que fosse dono de seu próprio destino e que superasse o colonialismo.

GADOTTI, Moacir. Paulo Freire : uma bibliografia. 

São Paulo: Cortez, 1996.

Com base no texto e nas ideias freireanas, avalie as asserções a seguir e a relação proposta entre elas.

I. Paulo Freire denunciou a opressão e a exclusão gerada pela supressão do direito à educação e à cidadania, defendendo a educação como uma empreitada coletiva.

PORQUE

II. A educação deve ser compreendida como um ato político, pois deve incentivar a reflexão e a ação consciente e criativa do sujeito em seu processo de libertação.

A respeito dessas asserções, assinale a opção correta.

A) As asserções I e II são proposições verdadeiras, e a II é uma justificativa correta da I.

B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.

C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.

D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.

E) As asserções I e II são proposições falsas.

GABARITO.

ENADE 2021 - QUESTÃO 33 - LICENCIATURA

O Decreto n. 5.626/2005, que dispõe sobre a Língua Brasileira de Sinais (Libras) considera a pessoa surda como aquela que, por ter perda auditiva, compreende e interage com o mundo por meio de experiências visuais. Em consonância com o decreto, nas escolas públicas em que há crianças surdas ou com deficiência auditiva matriculadas, faz-se necessário o desenvolvimento de práticas capazes de garantir o seu direito à educação.

Disponível em: http://www.planalto.gov.br/ccivil_03/_Ato2004-2006/2005/Decreto/D5626.htm.

Acesso em 20 abr. 2020 (adaptado).

Considerando as ações necessárias para a escola garanti r o direito à educação das crianças surdas, avalie as afirmações a seguir.

I. É necessário criar situações em sala de aula que promovam o convívio social entres as crianças, que estimule o respeito às diferenças, promovendo o reconhecimento das suas potencialidades e o desenvolvimento afetivo, cognitivo, linguístico e sociocultural.

II. A Libras deve ser assegurada como a primeira língua da criança surda, considerando-se a Língua Portuguesa, na modalidade escrita, como a segunda.

III. É fundamental disponibilizar intérpretes de Libras para as crianças surdas, e caso não seja possível, é preciso solicitar aos familiares que procurem outra escola mais preparada.

IV. A escola deve fomentar parcerias com os pais com o objetivo de acolhê-los e ajudá-los a constituir uma imagem positiva de seu filho surdo, auxiliando-o na compreensão da sua realidade.

V. Os professores precisam desenvolver, em relação aos alunos surdos, processos de avaliação mais subjetivos com foco nas dificuldades de aprendizagem desses alunos.

É correto apenas o que se afirma em

A) I e V.

B) II e III.

C) I, II e IV.

D) I, III, IV e V.

E) II, III, IV e V.

GABARITO.

ENADE 2021 - QUESTÃO 34 - LICENCIATURA

As percepções sobre o termo liderança revelam uma configuração ainda precária da realidade brasileira no campo da gestão escolar. As pesquisas internacionais apresentam uma gama significativa de resultados sobre o tema há, pelo menos, mais de duas décadas. Vale lembrar que os estudos sobre escolas eficazes, na sua maioria, apontam o efeito da liderança do gestor como um dos principais fatores explicativos dessa equação.

Um sobrevoo nos dados da pesquisa Olhares Cotidianos sobre a Gestão Escolar (OCGE), realizada com gestores e professores de seis escolas de um município brasileiro, permite identificar, de forma geral, noções sobre o termo, ao se solicitar ao grupo algum tipo de caracterização mais precisa de liderança:

"Isso aí é uma coisa que se tem ou não se tem." (Ana, Grupo Liderança).

"O dom da palavra, do convencimento..." (Andrea, Grupo Liderança).

"Carisma" (Cíntia, Grupo Liderança).

"A pessoa nasce com isso ou não." (Adriana, Grupo Liderança).

COELHO, F. M. O Cotidiano da Gestão Escolar: o método de caso na sistematização de problemas. 

educação & realidade, Porto Alegre, v. 40, n. 4, out./dez. 2015, p. 1.261-1.276 (adaptado).

Relacionando as ideias de liderança expostas pelas participantes da pesquisa sobre o exercício da gestão escolar, avalie as afirmações a seguir.

I. As respostas de Ana e Adriana reforçam as concepções defendidas pelas investi gaçõescientíficas do campo educacional contemporâneo sobre liderança, que afirmam que nem todos podem ser gestores escolares e que é preciso ter a qualidade de empreendedor para ocupar esse cargo. 

II. Ana e Cíntia expõem ideias que são coerentes com os estudos atuais sobre a prática da gestão escolar, pois enfatizam o estilo administrativo do gestor, que é um fator fundamental para se compreender a liderança e as suas relações com os objetivos educacionais das escolas.

III. Em suas respostas, Andrea e Cíntia expressam a ideia de liderança a parti r de um de seus aspectos, o interpessoal, embora outros fatores relevantes interfiram na gestão escolar, como o administrativo e/ou o pedagógico.

IV. As afirmações das participantes relacionam a liderança a uma capacidade de convencimento e a uma habilidade inata do líder – concepções já ultrapassadas pelas investigações educacionais sobre o tema no cenário contemporâneo.

É correto apenas o que se afirma em

A) I e IV.

B) II e III.

C) III e IV.

D) I, II e III.

E) I, II e IV.

GABARITO.

ENADE 2021 - QUESTÃO 35 - LICENCIATURA

As redes sociais promovem formas de interação entre indivíduos agrupados por interesses mútuos, identidades semelhantes e também por valores compartilhados. Nesse contexto, a Internet vem se tornando um importante espaço para movimentos sociais por possibilitar uma acelerada e ampla difusão de ideias e absorção de novos elementos em busca de algo em comum. Assim, o s movimentos sociais se fazem valer cada vez mais da “ democracia informaciona l”, da “ ciberdemocracia” e da prática do “ ciberativismo”. 

A parti r das ideias sobre comunicação e interação virtual, avalie as afirmações a seguir.

I. Os movimentos sociais tendem a perder força, prestígio e visibilidade com o crescimento da virtualidade junto à nova geração de jovens e adultos.

II. Ciberdemocracia, democracia informacional e ciberativismo podem ser classificados como movimentos advindos da virtualidade.

III. As redes sociais potencializam o ativismo fazendo uso da virtualidade, no entanto, ainda são pouco exploradas pelos movimentos sociais da atualidade.

IV. Tempo e espaço são conceitos a serem repensados a parti r da inserção cada vez maior da virtualidade na vida social.

V. É papel do educador formar e preparar os alunos para uma atuação responsável e crítica frente à virtualidade, explorando suas potencialidades.

É correto apenas o que se afirma em

A) I, II, e III.

B) I, III e IV.

C) I, IV e V.

D) II, III e V.

E) II, IV e V.

GABARITO.