Provas OBMEP 2021 com Gabarito e Resolução NÍVEL A OBMEP 2021 - QUESTÃO 01 Janaína escreveu a igualdade abaixo em uma folha de papel. Veio u...
Provas OBMEP 2021 com Gabarito e Resolução
NÍVEL A
OBMEP 2021 - QUESTÃO 01
Janaína escreveu a igualdade abaixo em uma folha de papel. Veio uma borboleta e pousou sobre um dos números da conta. Que número é esse?
A) 0
B) 5
C) 10
D) 15
E) 20
OBMEP 2021 - QUESTÃO 02
Felipe desenhou três triângulos, cinco quadrados e quatro círculos. Depois ele pediu para Anita apagar todas as figuras de quatro lados. Quantas figuras restaram?
A) 1
B) 4
C) 5
D) 6
E) 7
OBMEP 2021 - QUESTÃO 03
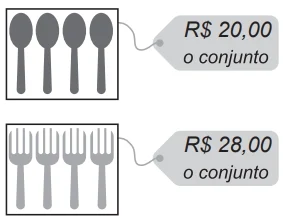
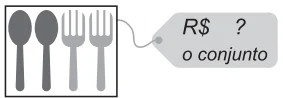
Veja os preços dos talheres.
Quanto custa, em reais, o conjunto de duas colheres e dois garfos?
A) 20
B) 22
C) 24
D) 26
E) 28
OBMEP 2021 - QUESTÃO 04
Mônica ganhou de presente 3 animais; ela contou todos os pés dos bichinhos e viu que totalizavam uma dezena. Quais animais Mônica pode ter ganhado?
A) 2 coelhos e 1 peixe.
B) 1 coelho e 2 passarinhos.
C) 2 coelhos e 1 passarinho.
D) 3 passarinhos.
E) 2 passarinhos e 1 peixe.
OBMEP 2021 - QUESTÃO 05
Seis pessoas esperam para entrar em um elevador, cuja carga máxima é de 180 quilos, para levá-las ao último andar. As pessoas pesam 50, 55, 60, 65, 70 e 75 quilos.
Qual é o menor número de viagens que o elevador deverá fazer para levar todas essas pessoas?
A) 2
B) 3
C) 4
D) 5
E) 6
OBMEP 2021 - QUESTÃO 06
Vovó Angélica fez uma torta para seus netinhos. Ela dividiu a torta em partes iguais e cada netinho comeu só um dos pedaços. O que restou da torta está mostrado na figura abaixo. Quantos são os netinhos da vovó Angélica?
A) 3
B) 4
C) 5
D) 6
E) 10
OBMEP 2021 - QUESTÃO 07
Em um depósito há uma sala com três armários. Em cada armário há quatro caixas e em cada caixa há 10 celulares. A sala, os armários e as caixas estão fechados, cada um deles com um cadeado. O encarregado, que está fora da sala, recebeu uma ordem para pegar 52 celulares. Quantos cadeados, no mínimo, ele terá que abrir?
A) 5
B) 6
C) 7
D) 8
E) 9
OBMEP 2021 - QUESTÃO 08
Uma andorinha, um bem-te-vi e um canário pousaram em três postes ao longo de uma rodovia. A andorinha pousou no poste que está a 380 m do início da rodovia; o bem-te-vipousou no poste que está a 450 metros do início da rodovia, bem no meio entre a andorinha e o canário.
A quantos metros do início da rodovia pousou o canário?
A) 410
B) 420
C) 510
D) 520
E) 900
OBMEP 2021 - QUESTÃO 09
Os sapatos de uma loja estão todos misturados e alguns estão sem par. Os sapatos são todos de mesmo modelo e cor. Para organizar a loja, Alice deve formar pares para colocar na vitrine, com um pé direito e um esquerdo, os dois com o mesmo número.
Quantos pares Alice pode formar?
A) 4
B) 5
C) 6
D) 7
E) 8
OBMEP 2021 - QUESTÃO 10
Na feira da cidade de Quixajuba,
• um pato custa o mesmo que duas galinhas;
• um leitão e três patos custam o mesmo que uma cabra;
• dois patos e duas galinhas custam o mesmo que um leitão.
Se Marco vender uma cabra, quantos patos ele poderá comprar com o dinheiro dessa venda?
A) 3
B) 4
C) 5
D) 6
E) 7
OBMEP 2021 - QUESTÃO 11
No tabuleiro abaixo, há oito peças. Cada uma delas pode ser deslocada para uma casa vizinha que não esteja ocupada. As peças podem ser movimentadas na horizontal, na vertical ou na diagonal. Cláudio deseja que apenas duas peças fiquem em cada linha e em cada coluna.
Qual é a menor quantidade de movimentos que Cláudio deve fazer?
A) 0
B) 1
C) 2
D) 3
E) 4
OBMEP 2021 - QUESTÃO 12
Miguel escolheu um número de três algarismos e outro número de dois algarismos. Ele viu que a diferença desses números era o maior resultado par possível.
Qual foi a diferença dos números que Miguel escolheu?
A) 898
B) 988
C) 990
D) 998
E) 999
OBMEP 2021 - QUESTÃO 13
Samuel numerou de 1 a 6 as faces de um cubo. Depois, ele verificou que a soma dos números em um par de faces opostas era 3. Ao verificar a soma dos números nos dois outros pares de faces opostas, qual dos números a seguir com certeza ele não achou?
A) 6
B) 7
C) 8
D) 9
E) 10
OBMEP 2021 - QUESTÃO 14
Algumas joaninhas grandes e pequenas estão fazendo uma festa. Joaninhas pequenas têm 5 pintas e joaninhas grandes têm 6 pintas.
Se o total de pintas na festa é 43, podemos dizer que nessa festa há exatamente:
A) 6 joaninhas.
B) 7 joaninhas.
C) 8 joaninhas.
D) 9 joaninhas.
E) 10 joaninhas.
OBMEP 2021 - QUESTÃO 15
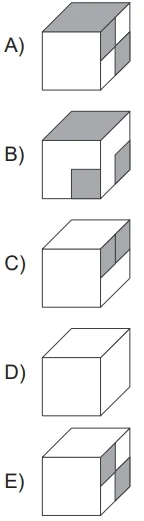
Paulinha quer recortar a figura abaixo, fazer as dobras e depois as colagens para obter um cubo.
Qual dos cubos abaixo ela irá obter?
NÍVEL 1
OBMEP 2021 - QUESTÃO 01
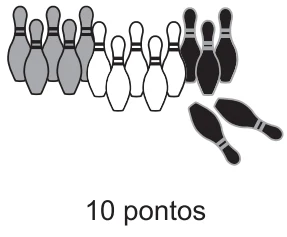
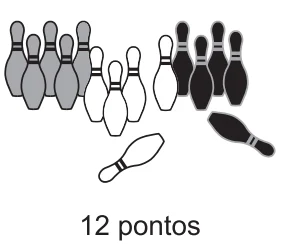
Mariana tem um jogo de 15 pinos, sendo 5 pretos, 5 brancos e 5 cinzas. Pinos de mesma cor valem o mesmo número de pontos. A pontuação obtida em uma jogada é a soma dos pontos correspondentes aos pinos derrubados.
Em uma jogada, Mariana fez 10 pontos ao derrubar dois pinos pretos. Em outra jogada, ela fez 12 pontos ao derrubar um pino preto e um branco. Numa terceira jogada, Mariana fez 55 pontos ao derrubar três pinos pretos, um branco e três cinzas.
a) Quantos pontos vale cada pino preto?
b) Quantos pontos vale cada pino cinza?
c) Mariana fez 42 pontos em uma jogada ao derrubar pelo menos um pino de cada cor. Quantos pinos de cada cor ela derrubou?
OBMEP 2021 - QUESTÃO 02
Em uma fila há 100 pessoas. A primeira e a terceira posições da fila são ocupadas por homens. A cada cinco posições consecutivas, há três mulheres e dois homens. Por exemplo, nas posições 13, 14, 15, 16 e 17, há três mulheres e dois homens.
a) Quantas mulheres há na fila?
b) Complete a tabela abaixo escrevendo homem ou mulher em cada posição, de acordo com o enunciado.
c) Complete a tabela abaixo escrevendo homem ou mulher em cada posição, de acordo com o enunciado.
OBMEP 2021 - QUESTÃO 03
Janaína desenha quadrados formados por quadrados menores, cujos lados têm medidas inteiras. Por exemplo, a figura mostra como Janaína desenhou um quadrado de lado 4 formado por dez quadrados, sendo dois de lado 2 e oito de lado 1.
a) Mostre como Janaína pode desenhar um quadrado de lado 3 formado com a menor quantidade possível de quadrados menores com lados de medidas inteiras.
b) Janaína quer desenhar um quadrado grande formado por um quadrado de lado 3, alguns quadrados de lado 2 e a menor quantidade possível de quadrados de lado 1. Mostre, no quadriculado ao lado, como Janaína pode fazer esse desenho.
c) Janaína quer desenhar um quadrado de menor lado possível formado por 13 quadrados de lado 1 e por outros quadrados maiores com lados de medidas inteiras. Mostre, no quadriculado ao lado, como Janaína pode fazer esse desenho.
OBMEP 2021 - QUESTÃO 04
Joãozinho fez todas as divisões possíveis com dois números diferentes pertencentes ao conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}. Por exemplo, com os números 2 e 5, ele fez as seguintes divisões: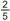 
(obteve como resultado 0,4) e 
(obteve como resultado 2,5).
(obteve como resultado 0,4) e (obteve como resultado 2,5).a) Em quantas divisões Joãozinho obteve como resultado um número inteiro?
b) Em quantas divisões Joãozinho obteve como resultado um número maior do que 0,5?
c) Quantos resultados diferentes foram obtidos por Joãozinho?
OBMEP 2021 - QUESTÃO 05
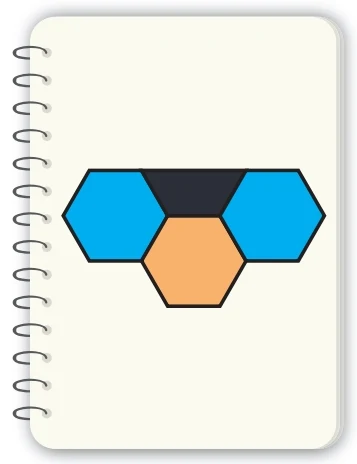
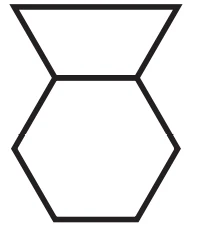
Maria pinta, em seu caderno, figuras formadas por trapézios e hexágonos. Cada hexágono pode ser pintado de azul, bege ou cinza, e cada trapézio, de azul ou preto. Polígonos com um lado em comum não podem ter a mesma cor. A figura ao lado é um exemplo de uma pintura feita por Maria.
a) De quantas maneiras Maria pode pintar a figura abaixo?
b) De quantas maneiras Maria pode pintar a figura abaixo?
c) De quantas maneiras Maria pode pintar a figura abaixo
OBMEP 2021 - QUESTÃO 06
Um dia é fantástico quando sua data, escrita na forma DD/MM/AA, contém todos os algarismos de 0 a 5. Por exemplo, o dia 12 de abril de 2053 será fantástico, pois sua data, 12/04/53, contém todos os algarismos de 0 a 5. Já o dia seguinte não será fantástico, pois sua data, 13/04/53, não contém o algarismo 2.
a) Qual será o último dia fantástico do ano de 2054?
b) Qual foi o primeiro dia fantástico depois de primeiro de janeiro de 2001?
c) Entre 2001 e 2100, quantos anos têm pelo menos um dia fantástico?
NÍVEL 2
OBMEP 2021 - QUESTÃO 01
Gabriel gosta de preencher quadriculados 3 × 3 com números de forma que quaisquer três deles, alinhados na horizontal, vertical ou diagonal, tenham a seguinte propriedade: o número central deve ser a média aritmética dos seus dois vizinhos.
a) Complete o preenchimento do quadriculado abaixo, iniciado por Gabriel.
b) Preencha o quadriculado abaixo seguindo a mesma instrução indicada anteriormente.
c) Qual será a soma dos nove números do quadriculado abaixo após Gabriel terminar de preenchê-lo?
OBMEP 2021 - QUESTÃO 03
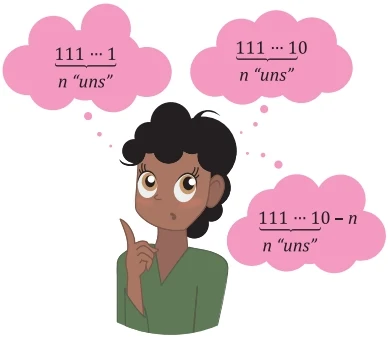
Julieta calcula as somas do tipo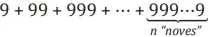 
da seguinte maneira: ela pensa no número 
multiplica-o por 10 e subtrai n.
da seguinte maneira: ela pensa no número multiplica-o por 10 e subtrai n. Por exemplo,
a) Calcule a soma 
da mesma maneira que Julieta.
da mesma maneira que Julieta.b) Quantos algarismos 0 há no resultado da soma 
c) Explique por que a maneira como Julieta calcula essas somas é correta.
OBMEP 2021 - QUESTÃO 05
A figura ao lado mostra um hexágono regular ABCDEF e os pontos médios P, Q, R, S e T dos lados AB, CD, DE, EF e FA, respectivamente.
a) Se a área do triângulo AST for igual a 1 cm², qual será a área do triângulo FTS?
b) Qual é a razão entre as áreas dos triângulos APR e PBQ?
c) Qual é a razão entre as áreas sombreada e não sombreada na figura abaixo?
OBMEP 2021 - QUESTÃO 06
Cinco pedras, A, B, C, D e E, estão dispostas como na figura. Kiko, o sapo simpático, pula de uma pedra para outra somente se elas estiverem ligadas por um segmento. Assim, ele pode pular, partindo de A, para B ou D, mas não para E ou C. Por exemplo, começando em A e terminando em D, ele pode realizar o seguinte passeio de 5 pulos: A → B → E → D → C → D.
a) Quantos são os passeios de três pulos que Kiko pode fazer começando em A e terminando em B?
b) Kiko quer fazer um passeio de 1001 pulos, começando em A. Em quais pedras ele poderá terminar esse passeio? Justifi que sua resposta.
c) Quantos são os passeios de 2020 pulos que Kiko pode fazer começando em A e terminando em C?
NÍVEL 3
OBMEP 2021 - QUESTÃO 03
Os números de 1 a 9 são distribuídos ao acaso e sem repetição nas casas do quadriculado desenhado na lousa ao lado.
a) Qual é a probabilidade de que a casa central seja preenchida com um número ímpar?
b) Qual é a probabilidade de que o quadriculado tenha uma coluna preenchida apenas com números pares?
c) Qual é a probabilidade de que o quadriculado tenha uma linha e uma coluna preenchidas apenas com números ímpares?
OBMEP 2021 - QUESTÃO 04
Uma lata medindo 20 cm × 10 cm × 10 cm, sem tampa, é sustentada por um suporte, de modo que uma de suas arestas mais curtas fique apoiada no plano horizontal e as arestas mais longas formem um ângulo de 45° com o plano horizontal, conforme mostra a figura. Suponha que um líquido seja colocado na lata, até a altura h em relação ao plano horizontal, também como indicado na figura.
a) Qual é o volume total da lata?
b) Explique por que a altura máxima que o líquido vai atingir é 10√2 cm e calcule o volume de líquido na lata quando essa altura é atingida.
c) Faça o gráfico da função V, que fornece o volume V(h) de líquido na lata, em cm³, quando sua superfície está na altura h, em cm.
OBMEP 2021 - QUESTÃO 05
Na figura, as circunferências de raios a e b, centradas em O e O’, são tangentes aos lados do ângulo em S e T e em S’ e T’, respectivamente. Elas também tangenciam os lados AB e AC de um triângulo ABC, em que A pertence a TT’ e BC está contido em SS’. Esse triângulo ABC tem altura h relativa à base BC.
a) Calcule o perímetro do triângulo ABC quando SS’ = 10.
b) Denote as áreas dos triângulos ABC, ABO e ACO’ por A1, A2 e A3, respectivamente. Explique por que a área do hexágono OSS’O’T’T é dada por A1 + 2A2 + 2A3.
c) Mostre que a área do triângulo ABC é 
d) Mostre que, se AB = AC, então h = a + b.
OBMEP 2021 - QUESTÃO 06
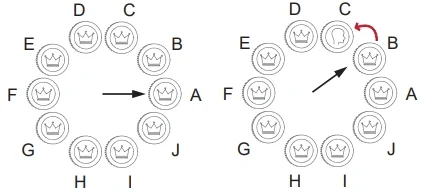
Em cada uma das dez posições marcadas com as letras de A a J na figura abaixo, é colocada uma moeda. Inicialmente, todas as dez moedas são colocadas com a face coroa voltada para cima e um ponteiro aponta para a posição A. Esse ponteiro começa a se movimentar no sentido anti-horário, saltando de uma posição para a outra mais próxima.
Após cada salto,
• se o ponteiro apontar para uma moeda com a face cara para cima, nada acontece;
• se o ponteiro apontar para uma moeda com a face coroa para cima, deve-se, então, virar a moeda seguinte.
Por exemplo, após o primeiro salto, o ponteiro aponta para a posição B (coroa) e a moeda na posição C é virada, ficando com a face cara para cima.
a) Como ficarão as moedas nas posições C e D logo após o segundo salto do ponteiro?
b) Em quais posições as moedas ficarão com as faces coroa para cima após o décimo segundo salto?
c) Explique por que nunca todas as moedas ficarão com a face cara voltada para cima.
d) Explique por que todas as moedas ficarão novamente com a face coroa voltada para cima após algum salto futuro do ponteiro.
COMENTÁRIOS