Prova Professor de Matemática IFPI 2022 com Gabarito

Concurso: IF-PI - 2022 - Professor - Edital nº 73

Órgão/Instituição: Instituto Federal de Educação Ciência e Tecnologia do Piauí

Banca/Organizadora: Instituto Federal de Educação, Ciência e Tecnologia do Piauí

Cargo: Professor - Matemática

Escolaridade: Superior

OBS: As questões de 01 à 20 são comuns a todas as demais provas desse concurso, com isso você as encontra NESTA PÁGINA!

CONHECIMENTO ESPECÍFICO

IFPI 2022 - QUESTÃO 21

Um professor dispõe de 20 questões, sendo 7 de funções reais, 3 de probabilidade, 5 de geometria e 5 de álgebra. De quantas maneiras distintas ele pode elaborar uma prova com 10 questões, de modo que essa prova contenha exatas quatro questões de funções reais, pelo menos duas de probabilidade e até duas de geometria?

a) 10.500

b) 13.125

c) 13.825

d) 14.175

e) 20.125

GABARITO.

IFPI 2022 - QUESTÃO 22

Observando uma roda gigante, um professor de Matemática notou que, a cada parada, uma determinada cadeira se colocava a uma distância do chão, modelada segundo a função periódica definida por

Sabendo que, na primeira parada (t = 1), o professor observou que a cadeira se encontrava a 2 m e, na segunda parada (t = 2), observa a altura de 5 metros, qual será a altura observada da cadeira quando a roda gigante fizer a 2022ª parada?

a) 0,6 m

b) 0,8 m

c) 2 m

d) 4 m

e) 5 m

GABARITO.

IFPI 2022 - QUESTÃO 23

Os membros do Clube do livro de um campus do interior do Instituto Federal do Piauí elegeram uma comissão para programar um passeio cultural de 3 dias, à cidade histórica de Ouro Preto. Após uma pesquisa de preços, a comissão divulgou a seguinte tabela com os custos da viagem:

Ficou decidido que o custo total seria dividido igualmente entre todos os membros; porém, ao saberem dos valores individuais, 10 membros desistiram, o que acarretou um aumento de R$ 550,00 para cada um dos que mantiveram o propósito de viajar. Quantos foram ao passeio?

a) 54

b) 50

c) 49

d) 44

e) 42

GABARITO.

Texto para a questão 24.

Quem nunca chutou a bola por cima do muro, para fora do campo ou do outro lado da rua?

Aconteceu com o Banks o'Dee FC, pequeno time fundado em 1902, na cidade de Aberdeen, leste da Escócia, e que participa apenas da divisão regional do país. A equipe sub-19 jogava, quando a bola voou por cima da cerca e aterrissou no Lago Dee.

Todos já haviam desistido dela quando, tempo depois, um e-mail chegou à diretoria do clube: "Olá! Um jogador de vocês com certeza tem um dos melhores chutes de longa distância do mundo!"

Quem assinava era Johnny Mikalsen, morador da ilha de Vanna, na Noruega, a quase 1.800 km de distância do campo do o'Dee.

"Um amigo meu achou a bola com o nome do clube escrito. Ela viajou uma boa distância; estamos a 1.118 milhas ao norte de Aberdeen, em uma ilha chamada Vanna, 10 km de Tromso, capital nortenha da Noruega."

Fonte: https://www.espn.com.br/blogs/olhaisso/686291_chute-mais

-longo-do-mundo-bola-vai-por-cima-da-cerca-e-e-encontrada

-em-outro-pais Acesso em: 04 jul. 2

IFPI 2022 - QUESTÃO 24

Exercitando nossa capacidade imaginativa, vamos considerar que a bola tenha sido literalmente chutada de Aberdeen (Sld) até Vanna (NO), formando uma parábola ligando um país ao outro. Considerando que a 600 quilômetros da ilha de Vanna a bola ainda estivesse a 40 quilômetros de altura, qual a altura h máxima alcançada, em quilômetros, pela bola, nessa hipotética viagem?

(OBS.: 1 milha vale aproximadamente 1,61 km)

a) 65

b) 60

c) 55

d) 50

e) 45

GABARITO.

Texto para a questão 25.

Estacionamentos, os novos vilões da mobilidade urbana.

Para urbanistas, o simples ato de procurar uma vaga e estacionar se tornou um risco para a sustentabilidade nas cidades.

Os urbanistas são unânimes em dizer que quanto mais espaços se criam para os carros, mais carros aparecem para ocupá-los.

Uma pesquisa da EY Consultoria, realizada para quantificar as vagas em 15 distritos do centro expandido da capital paulista, mostra que existe lugar para apenas 384 mil carros dos 509 mil que vão para a região diariamente.

Disponível em:https://exame.com/brasil/

estacionamentos-os-novos-viloes-

da-mobilidade-urbana/ Acesso em 04 jul. 2022.

IFPI 2022 - QUESTÃO 25

Imagine um empreendimento de parquímetros inteligentes para fazer cobrança variável das vagas, com base na demanda de certas regiões, nos horários de pico criados para suprir essa demanda reprimida, em apenas três dos 15 distritos apontados.

No distrito A, cobram-se R$ 17,00 por hora de permanência mais R$ 6,00 a cada 10 minutos adicionais. No distrito B, cobram-se R$ 10,00 a cada 20 minutos, onde minutos adicionais serão aproximados para 20.

No distrito C cobram-se R$ 18,00 por hora e R$ 0,50 por minuto adicional. Com base nesses dados apresentados, quais os menores valores cobrados, respectivamente, para quem estacionar 1 hora e 40 minutos e para quem estacionar 7 horas?

a) R$ 29,00 e R$ 126,00

b) R$ 41,00 e R$ 119,00

c) R$ 38,00 e R$ 119,00

d) R$ 29,00 e R$ 210,00

e) R$ 38,00 e R$ 210,00

GABARITO.

IFPI 2022 - QUESTÃO 26

A arte do ladrilhamento consiste no preenchimento do plano, por moldes, sem superposição ou buracos. Ela existe desde que o homem começou a usar pedras para cobrir o chão e as paredes de sua casa e continuou com a aplicação de cores, desenhos ou figuras para deixar os ladrilhos mais agradáveis.

Mosaicos quase-regulares ou arquimedianos são aqueles em que os ladrilhos são polígonos regulares. A intersecção de dois polígonos é sempre um lado ou um vértice ou vazia e o tipo de cada vértice é sempre o mesmo, isto é, a distribuição ao redor de cada vértice é sempre a mesma, sendo os polígonos regulares não necessariamente congruentes.

Disponível em:http://clubes.obmep.org.br/blog/wp-content/

uploads/2015/10/monografia2.pdf Acesso em 04 jul. 2022.

Considere que a padronagem a seguir foi usada para ladrilhar uma calçada de dimensões 1,60 m por 1,02 m. E utilizou hexágonos regulares de lado 20 cm.

Qual a área da calçada, em centímetros quadrados, coberta apenas por triângulos? (Considere √3 = 1,7)

a) 4080 cm²

b) 3400 cm²

c) 2700 cm²

d) 2040 cm²

e) 1380 cm²

GABARITO.

IFPI 2022 - QUESTÃO 27

A bandeira do estado do Piauí foi adotada em 24 de julho de 1922, através da Lei Estadual nº 1050. A bandeira possui formato retangular. Ela é composta por treze listras intercaladas, sendo 7 na cor verde e 6 na cor amarela. No canto superior esquerdo há um retângulo azul com uma estrela de cinco pontas branca ao centro do mesmo.

Abaixo da estrela, há a inscrição, na cor branca, da data "13 de março de 1823" (incluída em alteração de 2005). Esta é a data em que ocorreu a Batalha do Jenipapo, que foi importante no processo de Independência do Brasil. Ocorrida no território do Piauí, a batalha contou com cearenses, maranhenses e piauienses que lutaram contra tropas portuguesas contrárias à independência do Brasil.

Ocorrida no território do Piauí, a batalha contou com cearenses, maranhenses e piauienses que lutaram contra tropas portuguesas contrárias à independência do Brasil.

Disponível em: https://www.suapesquisa.com/

estadosbrasileiros/bandeira_piaui.htm

Acesso em: 04 jul. 2022.

A estrela da bandeira é Antares e é a estrela que representa o estado do Piauí na bandeira nacional. Segundo a Casa Civil Brasileira, as medidas de bandeiras no Brasil foram normatizadas por um tamanho padrão chamado "pano", que é igual à 0,64m de largura por 0,455m de altura. Os demais tamanhos são múltiplos ou submúltiplos deste padrão. Assim uma bandeira de 2 panos tem largura de 1,28 e altura de 0,91 metros.

Sendo a estrela Antares um pentagrama regular inscritível em uma circunferência de raio 0,14 metros, cujo lado mede 0,11 metros. A área da estrela de uma bandeira de 2 panos está:

(Considere sen 72º = 0,95 e cos 72º = 0,31).

a) entre 225 e 235 cm²

b) entre 236 e 245 cm²

c) entre 246 e 255 cm²

d) entre 256 e 265 cm²

e) entre 266 e 275 cm²

GABARITO.

Texto para questão 28.

O que é o filtro de ar do motor?

A função do filtro de ar do motor é filtrar as impurezas do ar que será misturado ao combustível pelo sistema de injeção eletrônica, para que assim a combustão ocorra corretamente no interior do motor.

O filtro de ar do motor fica sob o capô do carro, normalmente sobre o motor em uma carcaça plástica. Os formatos dessa carcaça e do filtro variam, dependendo do modelo e função, mas, em geral, são retangulares ou arredondadas.

O filtro de ar do motor funciona então como uma barreira contra as impurezas no caminho do ar até ele ser misturado com o combustível, no carburador ou na injeção eletrônica. Basicamente, a trajetória do ar começa com ele sendo aspirado pela tomada de ar na frente do veículo. Ele então passa por um duto e cai no filtro de ar, normalmente composto de espuma sintética.

Disponível em: https://blog.selfcar.com.br/2018/09/21/fi ltro-de-ar-do-motor/

Acesso em: 04 jul.2022.

O filtro de ar do motor funciona então como uma barreira contra as impurezas no caminho do ar até ele ser misturado com o combustível, no carburador ou na injeção eletrônica.

Disponível em: https://www.tuningparts.com.br/fi ltro-de-ar-motor-chevrolet-

s10-2-4-2-5-fl ex-2-8-diesel-12-mann-fi lter?_pid=lKtcc Acesso em: 04 jul.2022.

IFPI 2022 - QUESTÃO 28

Suponha que o filtro de ar da figura seja arredondado e feito de um poliuretano especial. Suas dimensões são de 40 mm de diâmetro interno, 80 mm de diâmetro externo e altura 300 mm. Se a massa do poliuretano utilizado na confecção do filtro for de 720 g, já descontada a parte plástica, qual a densidade do poliuretano do filtro em kg × m⁻³ ?

a) 6,37 × 10⁻³

b) 6,37 × 10⁻²

c) 6,37 × 10²

d) 6,37 × 10³

e) 6,37 × 10⁵

GABARITO.

IFPI 2022 - QUESTÃO 29

Entre 2003 e maio de 2015, o governo federal entregou mais de 1,1 milhão de cisternas de água para consumo humano, no semiárido, e 121,4 mil tecnologias sociais voltadas à produção de alimentos.

As cisternas - soluções simples para captar e armazenar água da chuva – amenizam os efeitos da seca prolongada. Com isso, é possível que uma família de cinco pessoas possa conviver com a estiagem por até oito meses.

Disponível em:https://www.gov.br/casacivil/pt-br/assuntos/noticias/2015/junho/

construcao-de-cisternas-prepara-agricultores-para-seca-no-semiarido. Acesso

em: 04 jul.2022.

As cisternas modernas são feitas de polietileno de alta resistência e permitem o armazenamento de água de chuva ou água potável.

Supondo que a água armazenada na cisterna seja própria para consumo humano e que cada pessoa necessite, em média, de 2400 ml de água potável por dia para sua sobrevivência, durante quantos meses uma família de 5 pessoas poderá se beneficiar, apenas para consumo, da água acumulada na cisterna, cujas dimensões são A = 1,50 m e B = 2,20 m, supondo-a cheia até o tampo e sem reabastecimento?

(Considere um mês com 30 dias e π = 3,14).

a) 3 meses

b) 6 meses

c) 9 meses

d) 10 meses

e) 15 meses

GABARITO.

Texto para questão 30.

O que é inflação?

Inflação é o nome dado ao aumento dos preços de produtos e serviços. Ela é calculada pelos índices de preços, comumente chamados de índices de inflação.

O IBGE produz dois dos mais importantes índices de preços: o IPCA, considerado o oficial pelo governo federal, e o INPC.

O IPCA/IBGE verifica as variações dos custos com os gastos das pessoas que ganham de um a quarenta salários mínimos nas regiões metropolitanas de Belém, Belo Horizonte, Curitiba, Fortaleza, Porto Alegre, Recife, Rio de Janeiro, Salvador, São Paulo, município de Goiânia e Distrito Federal.

O IPCA/IBGE mede a variação dos custos dos gastos, no período do primeiro ao último dia de cada mês de referência.

Adaptado de: http://www.idealsoftwares.com.br/indices/ipca_ibge.html.

Acesso em: 04 jul.2022.

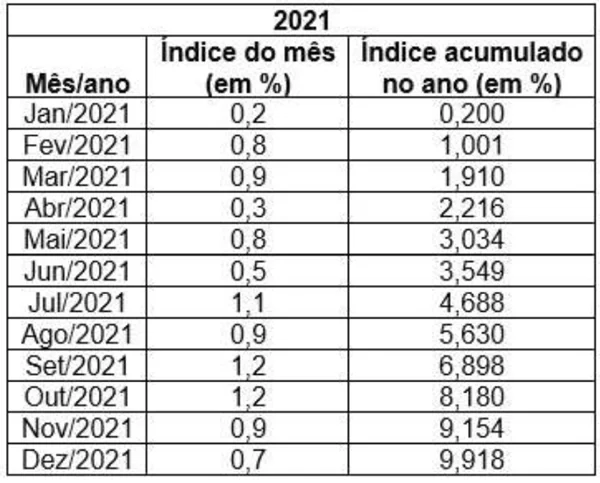
IFPI 2022 - QUESTÃO 30

Observando a tabela acima, qual a inflação acumulada no último trimestre de 2021, em percentual?

a) 4,090

b) 3,306

c) 3,020

d) 2,825

e) 1,920

GABARITO.

IFPI 2022 - QUESTÃO 31

De março de 2011 até junho de 2022, a Seleção Brasileira de Futebol masculino teve a seu favor 45 pênaltis marcados, e destes 51% foram batidos pelo jogador Neymar, totalizando 23 cobranças. Sabe-se que Neymar converteu 20 das 23 cobranças, obtendo assim um aproveitamento positivo de 87%.

Já, nos outros 22 pênaltis marcados a favor da Seleção Brasileira e batidos por outros jogadores, o aproveitamento foi de 68% de acertos, assim, os outros jogadores juntos marcaram 15 gols de pênalti, nesse mesmo período.

Considere que esses percentuais de aproveitamento se mantenham durante todo o ano de 2022. Se durante a Copa de 2022, no Catar, um pênalti for marcado a favor do Brasil e este for desperdiçado, qual a probabilidade de ser batido pelo Neymar?

a) 15,7%

b) 20,7%

c) 29,7%

d) 40,7%

e) 45,7%

GABARITO.

IFPI 2022 - QUESTÃO 32

Em 2021, devido às restrições e às medidas de distanciamento social, locais com auditórios tiveram que se adaptar e reduzir o número de lugares disponíveis para o público.

A direção de um teatro optou por não marcar as cadeiras indisponíveis, e sim, pedir ao público que escolham poltronas que não estejam próximas.

Dessa forma, foi colocado um comunicado na porta de entrada do teatro: “NENHUM ESPECTADOR PODE SENTAR-SE AO LADO DE OUTRO, SOB NENHUMA HIPÓTESE”. Se uma das fileiras desse teatro possui 16 poltronas alinhadas e consecutivas, de quantos modos 7 pessoas podem se distribuir nessa fileira, obedecendo o comunicado da direção do teatro?

a) 120

b) 2⁸ . 3² . 5² . 7 . 11 . 13

c) 11440

d) 3⁴ . 5 . 7 . 11 . 13

e) 8008

GABARITO.

Leia o texto, antes de responder à questão 33:

Desintegração radioativa

Os átomos de uma substância radioativa, como rádio ou urânio, possuem uma tendência natural a se desintegrarem, emitindo partículas e transformando-se em outra substância não radioativa. Assim, com o passar do tempo, a quantidade de substância original diminui. Isso é feito de tal maneira que, num determinado instante, a quantidade de matéria que se desintegra de um corpo radioativo é proporcional à massa da substância original presente no corpo naquele instante. A taxa de desintegração α é determinada experimentalmente e cada substância radioativa tem a sua taxa de desintegração, também chamada de constante de desintegração.

O modelo matemático abaixo é usado para cálculo da massa M(t) de uma substância radioativa após t intervalos de tempo, com taxa de desintegração α e M0 sua massa inicial:

IFPI 2022 - QUESTÃO 33

Sabendo que a meia-vida da substância radioativa rádio 228 gerada a partir da deterioração de urânio é de 6,7 anos, calcule o tempo aproximado necessário para que uma certa quantidade de massa do rádio 228 se reduza à 10% da quantidade inicial.

(Considere: ln2 = 7/10 e ln5 = 8/5).

a) Entre 12 e 13 anos

b) Entre 14 e 15 anos

c) Entre 19 e 20 anos

d) Entre 22 e 23 anos

e) Entre 25 e 26 anos

GABARITO.

IFPI 2022 - QUESTÃO 34

Uma rampa para manobras radicais foi construída, usando como modelo matemático para a sua descida a função do tipo exponencialf(x) = ax – 2 + b, com 0 < a < 1 e b > 0, até chegar em uma altura aproximadamente constante em relação ao solo. Após alguns metros, foi construída uma segunda rampa com declive linear e comprimento da base igual a 6 metros.

Sabe-se que a função f(x) passa pelos pontosH = (0, h), A = (1, 5), B = (2, 3) e C.

A partir do ponto C, inicia-se a segunda rampa, onde a medida do segmento CD, chamado de x, representa a medida da inclinação dessa rampa até o solo. Determine a altura máxima hda primeira rampa até o solo e a medida x da inclinação da segunda rampa.

a) h = 10m e x = 2 m

b) h = 9m e x = 2√5 m

c) h = 11m e x = 2√5 m

d) h = 10m e x = 2√10 m

e) h = 11m e x = 2√10 m

GABARITO.

IFPI 2022 - QUESTÃO 35

A Matemática é utilizada na programação linear para resolver problemas em diferentes áreas, em especial, nas atividades econômicas (comércio, prestação de serviços, indústrias, etc.), pois ela é fundamental nas tomadas de decisões, por exemplo, quando uma empresa quer definir a margem de lucro na venda de suas mercadorias.

Uma relojoaria franqueada a uma grande marca internacional vende no máximo 90 unidades de relógios dessa marca por mês, somados os modelos masculinos e os femininos.

A sua fornecedora exige que sejam vendidos pelo menos duas vezes mais relógios masculinos do que os modelos femininos. Sabendo que cada relógio masculino vendido gera um lucro de R$ 1.600,00, e a venda dos femininos traz um lucro de R$ 2.000,00 por unidade, determine o lucro máximo que essa relojoaria pode ter em um mês.

a) R$ 140.000,00

b) R$ 156.000,00

c) R$ 162.000,00

d) R$ 168.000,00

e) R$ 179.000,00

GABARITO.

IFPI 2022 - QUESTÃO 36

Uma pizza G, com a forma de uma circunferência de raio 20 cm, foi dividida em 10 fatias iguais. Todas estas fatias tem o formato próximo ao de triângulos isósceles, cujos lados iguais correspondem ao raio da pizza, conforme a ilustração abaixo. Determine a medida do lado da base desses triângulos.

a) 10 (√5 − 1) cm

b) 15 (√3 − 1) cm

c) (5√5 − 1) cm

d) 50 (√5 − 2) cm

e) 6(5√3 − 6) cm

GABARITO.

IFPI 2022 - QUESTÃO 37

O ITBI, Imposto Sobre Transmissão de Bens Imóveis, é um tributo municipal cobrado sempre que ocorre uma compra ou transferência de imóveis. Ele tem como fato gerador a transmissão entre pessoas vivas de propriedade ou domínio útil de bens imóveis, e tem como base de cálculo o valor venal do bem. Em Teresina-PI, atualmente a alíquota é de 3% para vendas de imóveis em áreas residenciais.

Seja um terreno, em Teresina-PI, que foi loteado em seis partes, conforme a figura acima, onde os pontos M, N, O, Q, R, S são os pontos médios dos lados AB, BC, CD, DE, EF e FA, respectivamente, e o ponto P a interseção comum dos segmentos MQ, NR e OS.

Na figura, temos ainda as áreas de cinco desses terrenos, determinados por quadriláteros.

São elas:

(PSAM) = 2946m², (PMBN) = 2789m², (PNCO) = 3578m², (PODQ) = 3321m², (PQER) = 2576m².

Calcule o ITBI a ser pago pelo comprador do terreno, determinado pelo quadrilátero PRFS, sabendo que o metro quadrado desse terreno custou R$ 100,00.

a) R$ 3.990,00

b) R$ 11.970,00

c) R$ 8.970,00

d) R$ 15.230,00

e) R$ 12.690,00

GABARITO.

IFPI 2022 - QUESTÃO 38

Uma fossa séptica é considerada uma pequena unidade de tratamento de esgoto doméstico, uma opção para residências onde ainda não existe saneamento básico. Nela, o esgoto passa por três etapas: na 1ª etapa, é encaminhado para um tanque impermeável, a fossa séptica em si, onde a matéria orgânica é depositada no fundo, formando um lodo que passará por um processo de degradação; na 2ª etapa, o líquido presente na fossa séptica irá passar por um filtro anaeróbico e, na 3ª etapa, será depositado no sumidouro, onde irá escoar o material, pois não possui fundo.

A imagem abaixo é de um projeto de fossa séptica, em formato de paralelepípedo de base quadrada ligada a um filtro anaeróbico cilíndrico, e este a um sumidouro também em formato cilíndrico.

No projeto, ficou estabelecido que os três têm a mesma altura de 11/π metros, e que a base da fosse séptica tem lado 2m. Sabe-se que o volume do filtro anaeróbio é a metade do volume da fossa séptica, e que o volume do sumidouro é o dobro do volume da fosse séptica. Sendo assim, determine a razão entre o raio da base do sumidouro e o raio da base do filtro anaeróbio.

GABARITO.

IFPI 2022 - QUESTÃO 39

João foi a uma concessionária comprar um carro novo. O modelo que ele escolheu custa R$ 78.750,00. O vendedor, Paulo, lhe apresentou duas opções de compras parceladas, ambas com 24 prestações fixas a serem pagas a partir do mês seguinte ao da compra.

Proposta I: sem entrada e com taxa de juros compostos de 2% ao mês.

Proposta II: com uma entrada de R$ 18.750,00 e com taxa de juros compostos de 1,8% ao mês. João, então, foi para casa calcular os valores totais nas duas propostas apresentadas por Paulo.

Usando 1,02²⁴ = 1,6 e 1,018²⁴ = 1,5 calcule a diferença aproximada dos valores totais a serem pagos nas duas propostas apresentadas por Paulo.

a) R$ 4.290,00

b) R$ 4.850,00

c) R$ 5.250,00

d) R$ 5.550,00

e) R$ 5.730,00

GABARITO.

IFPI 2022 - QUESTÃO 40

O método de integração tem sua origem no método da exaustão, o qual admite que uma grandeza possa ser subdividida indefinidamente e sua base seja a proposição: se de uma grandeza qualquer subtrai-se uma parte não menor que sua metade, do restante subtrai-se também uma parte não menor que sua metade, e assim por diante, se chegará, por fim, a uma grandeza menor que qualquer outra predeterminada da mesma espécie. Arquimedes aplicou este método para calcular a área de uma região limitada por um arco de parábola e pelo segmento que une as extremidades de tal arco (problema conhecido como a quadratura da parábola).

(EVENS, Howard. Introdução à história da Matemática. Editora Unicamp. 2004.)

Considere o arco de parábola 𝞿 de extremidades A e B e os pontos C, D, E de 𝞿, obtidos traçando-se os segmentos LC, MD, NE paralelos ao eixo focal da parábola, onde L, M, N são pontos médios dos segmentos AB, AC, BC, respectivamente (veja Figura 1). Denotando, de maneira geral, ∆ (vértices do triângulo) como área do triangulo de vértices destacados, Arquimedes mostrou que

Repetindo sucessivamente esse raciocínio, conclui-se que a área da região limitada pelo arco de parábola e pelo segmento AB (segmento parabólico) é dada por

Dada a parábola y = x² - 4x + 4 e seus pontos A(1,1) e B(4,4), o valor da área do segmento parabólico, em unidade de área, é:

GABARITO.

IFPI 2022 - QUESTÃO 41

Para vender bolas de basquete foram encomendadas embalagens unitárias em formato de tetraedros regulares, com a condição que partes de cada bola tenham suas superfícies externas à embalagem. Assim, cada bola terá quatro calotas esféricas idênticas à mostra, conforme a ilustração a seguir:

Considere que todas as bolas de basquete tenham o mesmo raio e que elas devem ser tangentes às arestas da embalagem em formato de tetraedro regular. Sabendo que o diâmetro de cada bola de basquete mede 72 cm, determine a medida da aresta de uma embalagem.

a) 36 √5 cm

b) 50 √3 cm

c) 54 √3 cm

d) 72 √2 cm

e) 144 √2 cm

GABARITO.

IFPI 2022 - QUESTÃO 42

Quando se entende parcialmente uma teoria, é possível que se chegue a muitos absurdos por inobservâncias das condições para aplicar determinados resultados matemáticos. Foi isso essencialmente o que aconteceu com a análise, durante o século seguinte à invenção do cálculo diferencial e integral, tendo como resultado uma acumulação de absurdos. Observe os procedimentos abaixo:

Considere a integral

Por outro lado,

Portanto,

Mas, por outro lado, sabemos que sen²x + cos²x = 1. Absurdo!

Marque a alternativa CORRETA que justifica a razão do absurdo demonstrado.

a) Os cálculos operacionais desenvolvidos na integral I1 não estão corretos.

b) Os cálculos operacionais desenvolvidos na integral I2 não estão corretos.

c) Os cálculos operacionais desenvolvidos nas integrais estão corretos, mas, nos resultados encontrados, as constantes devem ser diferentes e a diferença entre elas deve ser igual a 1 e não zero.

d) Os cálculos operacionais desenvolvidos nas integrais estão corretos, mas não vale o cancelamento das constantes nos dois membros.

e) Nenhuma das alternativas anteriores justifica a razão da contradição apresentada.

GABARITO.

IFPI 2022 - QUESTÃO 43

O desenvolvimento do cálculo diferencial teve suas origens no século XVII resultado de problemas sobre tangente à curvas e de questões de máximos e mínimos. Anos depois, foram desenvolvidas regras de derivação e derivada das principais funções elementares.

Faça a associação correta entre as duas colunas, relacionando a função à sua derivada correspondente.

Assinale a alternativa que apresenta a associação CORRETA entre números e letras:

a) 1-c, 2-a, 3-e, 4-b, 5-d

b) 1-b, 2-c, 3-e, 4-a, 5-d

c) 1-c, 2-e, 3-a, 4-b, 5-d

d) 1-c, 2-e, 3-a, 4-d, 5-b

e) 1-e, 2-c, 3-a, 4-b, 5-d

GABARITO.

IFPI 2022 - QUESTÃO 44

Seja a sequência (xn), cujo termo geral é dado por

onde k ∈ R, tal que 0 < k < 1. Sobre a convergência de (xn), é correto afirmar:

GABARITO.

IFPI 2022 - QUESTÃO 45

Seja T: R³ → R³ a rotação de um ângulo 0 em torno do eixo Z no sentido anti-horário, cuja matriz, em relação à base canônica do R³ é dada por

Considerando o ângulo

a respeito de T, é CORRETO afirmar:

a) T (1,0,0) = (1,0,0)

b) T (0,1,0) = (0,1,0)

c) T (0,0,1) = (1,0,1)

d) T (1,1,0) = (1,−1,0)

e) T (0,1,1) = (−1,0,1)

GABARITO.

IFPI 2022 - QUESTÃO 46

Seja T: R² → R² um operador linear tal que, para todo v = (x, y) ∈ R², o segmento de reta que liga V a T(x, y) = (x', y') é vertical e tem seu ponto médio sobre a reta y = x.

A alternativa que contém a expressão CORRETA do operador linear é:

a) T (𝑥,𝑦) = (𝑥, 2𝑥 + 𝑦)

b) T (𝑥,𝑦) = (𝑥, 2𝑦 + 𝑥)

c) T (𝑥,𝑦) = (𝑥, 2𝑥 − 𝑦)

d) T (𝑥,𝑦) = (𝑥, 2𝑦 − 𝑥)

e) T (𝑥,𝑦) = (𝑥, 2𝑥 − 2𝑦)

GABARITO.

IFPI 2022 - QUESTÃO 47

Dada a elipse

qual o valor da área (em unidades de área u.a) do triângulo determinado pelos pontos A(0,0),B(-10,0) e C(xc,yc),yc > 0, onde C é o ponto de tangência da reta que passa por B com a elipse E?

a) 6

b) 7

c) 8

d) 9

e) 10

GABARITO.

IFPI 2022 - QUESTÃO 48

Seja

um vetor de módulo igual a √3 e

um outro vetor, no mesmo espaço, com módulo unitário. Qual o menor ângulo entre os vetores

para que a projeção ortogonal de

na direção de

seja igual

a) 30°

b) 120°

c) 135°

d) 150°

e) 165°

GABARITO.

IFPI 2022 - QUESTÃO 49

Os termos (x1, x2, x3, ..., x40) formam uma progressão aritmética de termos positivos e razão r < 0. Considere que a primeira metade desses termos foram agrupados em um grupo A e a segunda metade em grupo B1, com média igual a

Se o menor dos termos do grupo A passar para o grupo B1, formando o grupo B2, passando a ter uma nova média

o que podemos dizer sobre as médias aritméticas dos grupos B1 e B2?

a) A média

diminuiu em comparação com a média

porque recebeu o menor elemento do grupo A.

b) A média

aumentou em |r| em comparação com a média

c) A média

aumentou em

em comparação com a média

d) A média

aumentou em

em comparação com a média

e) A média

aumentou em

em comparação com a média

GABARITO.

IFPI 2022 - QUESTÃO 50

Em todas as n edições de elaboração de provas de concurso realizadas pela instituição Y, foi observada a seguinte distribuição do número de erros por edições de concurso:

Sabendo que a medida de variabilidade variância foi de , pode-se estimar que o número de edições com apenas um erro foi igual a:

a) 10

b) 15

c) 12

d) 17

e) 8

GABARITO.

IFPI 2022 - QUESTÃO 51

Considere a sequência decrescente e finita,

onde n é um número natural. Se a mediana dos elementos dessa sequência é 54, então, o valor de n é igual a:

a) 6

b) 5

c) 4

d) 3

e) 2

GABARITO.

IFPI 2022 - QUESTÃO 52

Entre os 20 estudantes de uma turma, foi construído um gráfico que indica o número de faltas que eles tiveram, no último mês.

Desse modo, o valor da variância populacional correspondente ao número de faltas dos estudantes é igual a:

a) 1,10263

b) 1,01026

c) 1,00475

d) 1,04750

e) 1,10000

GABARITO.

IFPI 2022 - QUESTÃO 53

Se uma elipse tem focos nos pontos F1 = (−1,1) e F2 = (1,2) e o comprimento do seu eixo maior é 2a = 4, então sua equação é dada pela expressão:

a) 80x²+68y²+ 16xy–24x–332y+41=0

b) 80x²–68y²–16xy–24x–170y–61=0

c) 48x²–60y²–16xy+26x+180y–41=0

d) 48x²+60y²– 16xy+24x–180y–41=0

e) 80x²+60y²+ 16xy–24x–180y–61=0

GABARITO.

IFPI 2022 - QUESTÃO 54

A reta que contém o ponto A=(1,-2,3) e é concorrente com as retas reversas r : X = (1, -1,3) + λ1 (1, 0, 2); λ1 ∈ R e s : X = (2, 1, 0) + λ2 (0, 1, 4); λ2 ∈ R, tem equação vetorial igual a:

a) X = (1, -2,3) + λ (-4, -17, -8); λ ∈ R

b) X = (1, -2,3) + λ (-5, -17, -8); λ ∈ R

c) X = (1, -2,3) + λ (-5, -11, -9); λ ∈ R

d) X = (1, -2,3) + λ (-4, -11, -8); λ ∈ R

e) X = (1, -2,3) + λ (-5, -17, -9); λ ∈ R

GABARITO.

IFPI 2022 - QUESTÃO 55

Uma superfície é obtida pela rotação da curva y : 3x + y + z = 1 e 2x - y + 3z = 2, quando gira em torno do eixo e : X = (1, 1, 1) + λ(1, 1, 1); λ ∈ R.

A equação dessa superfície é igual a: