Prova Matemática (Bacharelado e Licenciatura) ENADE 2017 com Gabarito
Prova Matemática (Bacharelado e Licenciatura) ENADE 2017 com Gabarito
OBS: as questões de 01 a 08 são de Formação Geral, portanto, cobradas em todas as provas. Para conferir elas, basta acessar essa página.
CONHECIMENTO ESPECÍFICO
BACHARELADO
QUESTÃO 09
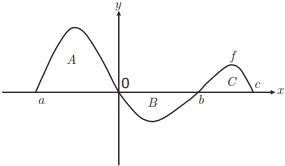
ENADE 2017: Considere f:[a,c] → R uma função contínua e b E (a,c), conforme ilustra o gráfico abaixo.
Represente por:
A a área da região limitada pela reta de equação
y = 0 e pela curva {(z,f(x); x E [a,0]}
B a área da região limitada pela reta de equação
y = 0 e pela curva {(x,f(x)); x E [0,b]};
C a área da região limitada pela reta de equação
y=0 e pela curva {(x,f(x)); x E [b.c]}.
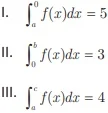
É correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 10
ENADE 2017: Considere uma urna com 5 bolas azuis, 3 verdes e 6 pretas, da qual serão retiradas bolas sem reposição. Com base nessa situação, avalie as afirmações a seguir.
I. Caso sejam retiradas 4 bolas, uma delas será verde.
II. O número mínimo de bolas que devem ser retiradas para se garantir a retirada de uma bola preta é igual a 9.
III. O número mínimo de bolas que devem ser retiradas para se garantir a retirada de uma bola verde e uma bola azul é igual a 10.
É correto o que se afirma em
A) II, apenas.
B) III, apenas.
C) I e II, apenas.
D) I e III, apenas.
E) I, II e III.
QUESTÃO 11
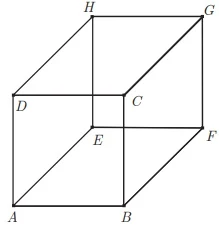
ENADE 2017: Considere o cubo de vértices A, B, C, D,E,F, G e H, ilustrado na figura abaixo, e os vetores b, c d, e, f, g e h, todos com origem em A e extremidades respectivamente em B, C, D, E, F, G e H.
Com base nas informações apresentadas, é correto afirmar que o vetor cujo produto escalar com f é igual a zero é o vetor
A) b.
B) c.
C) d.
D) g.
E) h.
QUESTÃO 12
Para calcular o limite 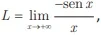 os argumentos podem ser desenvolvidos usando as desigualdades
os argumentos podem ser desenvolvidos usando as desigualdades 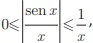 válidas para todo real x > 0.
válidas para todo real x > 0.
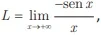 os argumentos podem ser desenvolvidos usando as desigualdades
os argumentos podem ser desenvolvidos usando as desigualdades 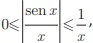 válidas para todo real x > 0.
válidas para todo real x > 0.ENADE 2017: A partir desses argumentos, conclui-se que L é igual a
A) -1
B) 0
C) 1
D) ∞
E) -∞
QUESTÃO 13
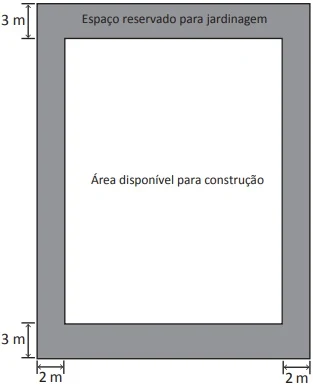
ENADE 2017: Uma construtora, com o objetivo de valorizar as áreas verdes, apresentou um projeto de loteamento, com terrenos retangulares, onde cada residência construída terá um jardim ao seu redor. Em cada terreno deverão ser reservados 3 metros na frente, 3 metros no fundo e 2 metros em cada lateral para jardinagem, conforme ilustra a figura a seguir.
Considerando-se que área disponível para construção será de 600 m², a área mínima do terreno que atende às especificações exigidas pela construtora será de
A) 606 m².
B) 610 m².
C) 726 m².
D) 864 m².
E) 921 m².
QUESTÃO 14
ENADE 2017: A respeito de transformações lineares no plano, avalie as afirmações a seguir.
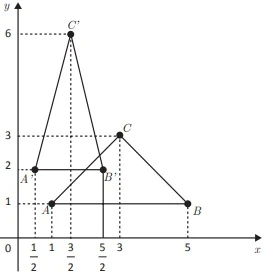
I. Sabendo que uma transformação de escala é um operador linear no plano cartesiano que multiplica a abscissa x de um ponto por um fator m e sua respectiva ordenada y por um fator n, a matriz associada à transformação de escala que leva, na figura a seguir, o triângulo ABC ao triângulo A'B'C' tem determinante igual a  .
.
 .
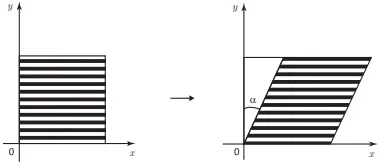
.II. A transformação linear que leva a região plana hachurada do gráfico à esquerda na região hachurada do gráfico à direita é dada por T(x,y) = (x,y + x tg α).
III. Na figura a seguir, a matriz da transformação linear que efetua a mudança do triângulo à esquerda para a posição mostrada à direita é  .
.
 .
.É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 15
ENADE 2017: O gerente de um posto de combustíveis observou que, na primeira semana do mês em que definiu o preço do litro de gasolina a R$ 3,70, foram vendidos 15 000 litros diários. Com isso, o posto fez uma promoção e percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 200 litros de gasolina a mais por dia.
Representando por p a quantidade de centavos correspondente ao desconto dado no preço de cada litro de gasolina, e por F o valor, em reais, faturado por dia com a venda de gasolina, a expressão que descreve essa situação é
A) F = 15 000 + 590p - 2p²
B) F = 15 000 + 590p + 2p²
C) F = 55 500 - 590p - 2p²
D) F = 55 500 + 590p - 2p²
E) F = 55 500 - 590p + 2p²
QUESTÃO 16
ENADE 2017: A solução de um sistema linear de três equações e três incógnitas pode ser interpretada geometricamente como a interseção de três planos no espaço e consiste em verificar se os três planos têm um único ponto, infinitos pontos ou nenhum ponto em comum, para determinar se o sistema possui solução única, infinitas soluções ou nenhuma solução, respectivamente.
Com base nessas informações, conclui-se que o sistema linear
tem como solução
A) o ponto (0,-1,3).
B) o plano que passa pelo ponto (0,-1,3) e que possui como vetor normal o vetor  =(1,2,1).
=(1,2,1).
 =(1,2,1).
=(1,2,1).C) a reta que passa pelo ponto (0,-1,3) e que possui como vetor diretor o vetor 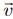 = (1,2,-1).
= (1,2,-1).
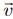 = (1,2,-1).
= (1,2,-1).D) a reta que passa pelo ponto (0,-1,3) e que possui como vetor diretor o vetor 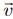 = (1,-1,1).
= (1,-1,1).
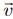 = (1,-1,1).
= (1,-1,1).E) o conjunto vazio.
QUESTÃO 17
ENADE 2017: Considere o conjunto A = (n e N:1 ≤ n ≤ 2017) = (1,2,...,2017).
O número de elementos de À que são múltiplos de 4 ou 6 é igual a
A) 840.
B) 756.
C) 672.
D) 168.
E) 84.
QUESTÃO 18
ENADE 2017: Em uma circunferência de centro O e raio 3, traça-se uma corda AB tal que 

Considerando que AC é um diâmetro dessa circunferência, quais são as medidas dos segmentos AB e BC, respectivamente?
A) 2√7 e 2√2.
B) 2 e 4√2.
C) 4√2 e 4√2.
D) 4√2 e 7.
E) 4√2 e 2.
QUESTÃO 19
ENADE 2017: De acordo com a Política Nacional de Resíduos Sólidos, a implantação da coleta seletiva é obrigação dos municípios, e metas referentes à coleta seletiva fazem parte do conteúdo mínimo que deve constar nos planos de gestão integrada de resíduos sólidos dos municípios.
Disponível em: <http://www.mma.gov.br>.“Acesso em: 10 jul. 2017 (adaptado).
Suponha que os prefeitos de três cidades vizinhas decidiram fazer um projeto conjunto para a construção de um armazém para separação de materiais recicláveis e que pudesse funcionar também como um ponto de entrega voluntária.
Os prefeitos decidiram que o armazém deveria ser construído em um local equidistante aos centros das cidades, representados em um plano cartesiano pelos pontos A = (1,3), B=(10,0) e C=(3,7).
Nessa situação, quais são as coordenadas do ponto escolhido?

QUESTÃO 20
ENADE 2017: Durante o final de temporada de um evento de corrida automobilística, é comum chover nos dois dias de treino, sexta-feira e sábado, e no dia da corrida, domingo. Suponha que a previsão meteorológica para esses dias indique 80% de chance de chuva para cada um dos dias de treino e 30% de chance de chuva para o dia da corrida.
Considerando as informações do texto acima, avalie as afirmações a seguir.
I. A chance de não chover em nenhum dos três dias é de 2,8%.
II. A chance de chover em pelo menos um dos três dias é de 97,2%.
III. A chance de chover sexta-feira e sábado é de 80%.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 21
ENADE 2017: Seis estudantes se inscreveram para um campeonato escolar de xadrez: três meninas, das quais duas são irmãs gêmeas, e três meninos.
Na primeira rodada serão formadas as três duplas de adversários por sorteio, da seguinte forma: o primeiro jogador é sorteado entre os seis participantes; o segundo é sorteado entre os cinco restantes; o terceiro entre os quatro restantes; o quarto, entre os três restantes; a primeira dupla é formada pelo primeiro e segundo sorteados; a segunda dupla é formada pelo terceiro e quarto sorteados; a terceira dupla é formada pelos dois últimos que não foram sorteados.
Considerando essas condições a respeito da formação das duplas de adversários na primeira rodada do campeonato, avalie as afirmações a seguir
I. A probabilidade de as gêmeas se enfrentarem é de 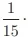
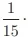
II. A probabilidade de a primeira dupla sorteada ser de meninos é de 

III. A probabilidade de a primeira dupla sorteada ser composta por uma menina e um menino é de 

É correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 22
ENADE 2017: Considere duas pirâmides, uma de base triangular e outra de base quadrada, ambas com a mesma altura e a mesma área da base, apoiadas em um plano α.
Assumindo que qualquer plano de corte B, paralelo a a, determina nos dois sólidos seções de mesma área, pode-se concluir que a relação entre o volume V1, da pirâmide de base triangular e o volume V2, da pirâmide de base quadrada é
A) 4V1 = 3V2
B) 3V1 = 3V2
C) V1=2V2
D) 2V1 = V2
E) V1 = V2
QUESTÃO 23
ENADE 2017: Considerando que um estudante esteja testando um software para calcular o valor da integral 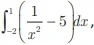 avalie as asserções a seguir e a relação proposta entre elas.
avalie as asserções a seguir e a relação proposta entre elas.
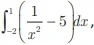 avalie as asserções a seguir e a relação proposta entre elas.
avalie as asserções a seguir e a relação proposta entre elas.I. O resultado 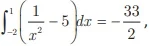 apresentado pelo software, está correto.
apresentado pelo software, está correto.
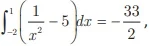 apresentado pelo software, está correto.
apresentado pelo software, está correto.PORQUE
II. A primitiva da função 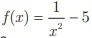 , e a função
, e a função 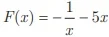 e, pelo Teorema Fundamental do
e, pelo Teorema Fundamental do
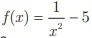 , e a função
, e a função 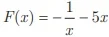 e, pelo Teorema Fundamental do
e, pelo Teorema Fundamental doCálculo, conclui-se que
A respeito dessas asserções, assinale a opção correta.
A) As asserções I e II são proporções verdadeiras, e a II é uma justificativa correta da I.
B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.
C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
E) As asserções I e II são proposições falsas.
QUESTÃO 24
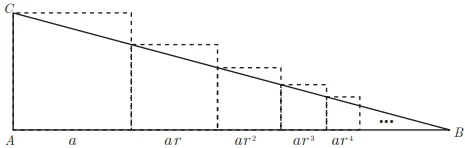
ENADE 2017: A figura a seguir mostra um triângulo retângulo de vértices A, B e C com catetos medindo α e α + αr + αr² + αr³ + ..., em que |r| < 1.

QUESTÃO 25
ENADE 2017: Considere n ≥ 2 um número inteiro. Com relação ao máximo divisor comum (mdc) entre n² - n + 1 e n + 1, avalie as afirmações a seguir.
I. Se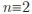 (mod 3),então mdc(n²-n+1,n+1)=3.
(mod 3),então mdc(n²-n+1,n+1)=3.
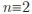 (mod 3),então mdc(n²-n+1,n+1)=3.
(mod 3),então mdc(n²-n+1,n+1)=3.II. Se n for par então mdc(n²-n+1,n+1)=1.
III. O resto da divisão de n²-n+1 por n+1 é n.
É correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 26
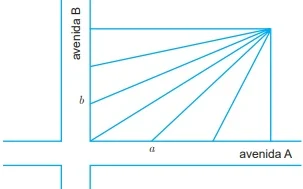
ENADE 2017: Um terreno plano em formato retangular fica no cruzamento de duas avenidas, sendo que o lado de medida a, voltado para a avenida A, é maior que o lado de medida b , voltado para a avenida B.
Esse terreno deve ser dividido entre seis herdeiros, de forma que, após a divisão, cada parte possua a frente voltada a uma destas avenidas, por onde se terá acesso direto.
A partir da divisão do lado a em três partes iguais e do lado b em outras três partes iguais, são propostos seis terrenos de formato triangular, conforme ilustra a figura a seguir.
A respeito dessa divisão, conclui-se que os terrenos
A) cujo acesso se dá pela avenida A têm área maior que aqueles cujo acesso se dá pela avenida B.
B) cujo acesso se dá pela avenida B têm área maior que aqueles cujo acesso se dá pela avenida A.
C) têm a mesma área, mas aqueles cujo acesso se dá pela avenida A têm sua frente maior que aqueles cujo acesso se dá pela avenida B.
D) têm a mesma área, mas aqueles cujo acesso se dá pela avenida B têm sua frente maior que aqueles cujo acesso se dá pela avenida A.
E) têm a mesma área, e aqueles cujo acesso se dá pela avenida A têm sua frente com a mesma medida que aqueles cujo acesso se dá pela avenida B.
QUESTÃO 27
ENADE 2017: Considere a sequência de números reais
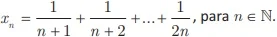
I. A sequência (xn) n E N é divergente, mas possui subsequência convergente.
II. A sequência (xn)n E N satisfaz a condição de Cauchy, ou Seja, dado ꞓ > O, existe um número natural M(ꞓ) tal que, para quaisquer m, n > M(ꞓ) , tem-se | xm -xn| < ꞓ.
III. O limite da sequência (xn)n E N é o supremo do conjunto {xn: n E N}.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 28
ENADE 2017: Considere T(t) a temperatura da água em um recipiente t segundos após o conjunto recipiente/ água ter sido colocado numa estufa, em cujo interior a temperatura é A. Segundo a lei do resfriamento de Newton, a taxa de variação da temperatura T(t) da água é proporcional à diferença entre T(t) e A.
Nessa situação, avalie as asserções a seguir e a relação proposta entre elas.
I. A lei física em questão é traduzida em linguagem “matemática pela equação diferencial T'(t) = -k [T(t) — A] , na qual k é uma constante positiva.
PORQUE
II. Se T(t) > A, então T'(t) <0, caso em que a temperatura T(t) é uma função decrescente de t e a água está resfriando; por outro lado, se T(t) < A, então T'(t) > 0, caso em que a temperatura T(t) é uma função crescente de t e a água está aquecendo.
A respeito dessas asserções, assinale a opção correta.
A respeito dessas asserções, assinale a opção correta.
A) As asserções I e II são proporções verdadeiras, e a II é uma justificativa correta da I.
B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.
C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
E) As asserções I e II são proposições falsas.
QUESTÃO 29
ENADE 2017: Sobre sequências de números reais, avalie as afirmações a seguir.
I. Toda sequência de números reais limitada é convergente.
II. Toda sequência de números reais convergente é monótona e limitada.
III. O conjunto de todas as sequências de números racionais que possuem apenas um número finito de termos diferentes de zero é enumerável.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III
QUESTÃO 30
ENADE 2017: Um operador linear definido em um espaço vetorial de dimensão finita pode ser representado por uma matriz quadrada.
Dado V, um espaço vetorial, e 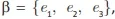 uma base para esse espaço, seja o operador linear T : V → V definido por
uma base para esse espaço, seja o operador linear T : V → V definido por 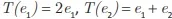 e
e 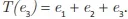 Considerando esse operador linear e a matriz A a ele associada na base dada, avalie as afirmações a seguir.
Considerando esse operador linear e a matriz A a ele associada na base dada, avalie as afirmações a seguir.
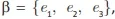 uma base para esse espaço, seja o operador linear T : V → V definido por
uma base para esse espaço, seja o operador linear T : V → V definido por 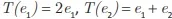 e
e 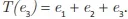 Considerando esse operador linear e a matriz A a ele associada na base dada, avalie as afirmações a seguir.
Considerando esse operador linear e a matriz A a ele associada na base dada, avalie as afirmações a seguir.I. Tem-se que (2I - A) (I-A)² = 0, em que I é a matriz identidade.
II. Tem-se que (2I - A) (I-A) = 0,em que I é a matriz identidade.
III. O operador T é diagonalizável.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 31
ENADE 2017: Diz-se que os grupos G1 e G2 são isomorfos quando existe um homomorfismo bijetor f: G1 → G2. Grupos isomorfos, ainda que possuam elementos de naturezas distintas, são considerados indistinguíveis do ponto de vista algébrico.
Considere os seguintes grupos:
Zm, o grupo aditivo das classes residuais módulo m;
Dn, o grupo das simetrias espaciais de um polígono regular de n lados munido da operação de composição.
Nesse contexto, avalie as afirmações a seguir.
I. Z2 x Z3, é isomorfo a Z6.
II. D3 é isomorfo a Z6.
III. D6, é isomorfo a Z6.
É correto o que se afirma e
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 32
ENADE 2017: A filial de uma empresa precisa contratar 40 funcionários para o setor produtivo e é necessário que esses profissionais realizem as tarefas rapidamente. Assim, o gestor responsável optou por um processo de seleção que exige dos candidatos a realização de uma tarefa em menos de 20 minutos.
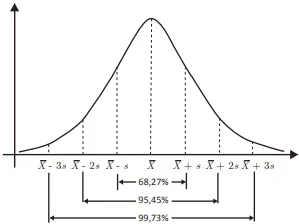
Para realizar previsões estatísticas, o gestor costuma levar em conta os percentuais associados a qualquer população com distribuição normal, com base em determinados intervalos gerados a partir da média 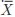 e do desvio-padrão s, conforme ilustra a figura a seguir.
e do desvio-padrão s, conforme ilustra a figura a seguir.
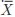 e do desvio-padrão s, conforme ilustra a figura a seguir.
e do desvio-padrão s, conforme ilustra a figura a seguir.Durante o processo de seleção, o gestor verificou que a média dos tempos de realização das tarefas pelos candidatos foi de 30 minutos, distribuídos normalmente, com desvio-padrão de 5 minutos. Por necessitar saber com rapidez uma estimativa da quantidade de aprovados, ele decidiu considerar apenas a parte inteira dos percentuais apresentados no gráfico da curva normal: 68%, 95% e 99%.
Após analisar apenas esses dados, e considerando que houve 1000 candidatos, o gestor deve concluir que a expectativa de contratação de 40 funcionários
A) será atingida, pois os dados indicam que 300 inscritos efetuaram a tarefa em vinte minutos ou menos.
B) será atingida, pois os dados indicam que 160 inscritos efetuaram a tarefa em vinte minutos ou menos.
C) será atingida, pois os dados indicam que 50 inscritos efetuaram a tarefa em vinte minutos ou menos.
D) não será atingida, pois os dados indicam que apenas 25 inscritos efetuaram a tarefa em vinte minutos ou menos.
E) não será atingida, pois os dados indicam que apenas 5 inscritos efetuaram a tarefa em vinte minutos ou menos.
QUESTÃO 33
ENADE 2017: Sejam S¹ = {(x, y) ꞓ R² : x² + y² = 1} e f: S¹ → R² uma aplicação contínua.
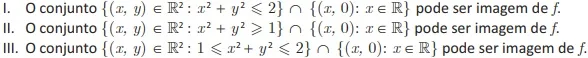
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III
QUESTÃO 34
ENADE 2017: A respeito das funções f1 : C → C, f2: C → C e f3: C → C, definidas por 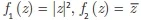 e
e 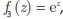 avalie as afirmações a seguir.
avalie as afirmações a seguir.
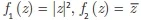 e
e 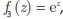 avalie as afirmações a seguir.
avalie as afirmações a seguir.I. A função f1 é analítica.
II. A função f2 é analítica.
III. A função f3 é analítica.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III
QUESTÃO 35
ENADE 2017: Considere 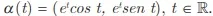
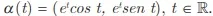
Nesse contexto, avalie as afirmações a seguir.
I. A curvatura da curva α é constante.
II. 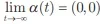
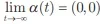
III. 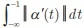 é finita.
é finita.
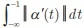 é finita.
é finita.É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e II, apenas.
D) II e III, apenas.
E) I, II e III.
LICENCIATURA
QUESTÃO 27
ENADE 2017: A etnomatemática é uma tendência em educação matemática que investiga, entre outras coisas, saberes matemáticos presentes em diferentes grupos culturais.
Os dois procedimentos descritos a seguir, utilizados por grupos de agricultores para calcular a área de uma região com a forma de um quadrilátero qualquer, podem ser considerados como exemplos dessa tendência.
Procedimento 1
Obtêm-se as duas médias aritméticas dos lados opostos do quadrilátero e multiplica-se um valor pelo outro.
Procedimento 2
Obtém-se a média aritmética do comprimento de todos os lados e multiplica-se esse valor por ele mesmo.
KNUNIK, G. À matemática da cubação da terra. Scientific American
Brasil, p. 86-90, 2006 (adaptado).
Em relação ao exemplo descrito, conclui-se que
A) o procedimento 1 permite calcular com exatidão a área da região limitada por um quadrilátero qualquer.
B) o procedimento 2 permite calcular com exatidão a área da região limitada por um quadrilátero qualquer.
C) os procedimentos 1 e 2 fornecem o mesmo valor para a área, caso o quadrilátero seja um trapézio.
D) os procedimentos 1 e 2 fornecem o mesmo valor para a área, caso o quadrilátero seja um retângulo.
E) os procedimentos 1 e 2 fornecem o mesmo valor para a área, caso o quadrilátero seja um quadrado.
QUESTÃO 28
ENADE 2017: É preciso repensar certas ideias predominantes acerca da avaliação em matemática, ou seja, ideias que concebem como prioritário avaliar apenas se os alunos memorizam as regras e os esquemas, não verificando a compreensão dos conceitos, o desenvolvimento de atitudes e procedimentos e a criatividade nas soluções, que, por sua vez, se refletem nas possibilidades de enfrentar situações- problema e resolvê-las.
As formas de avaliação devem contemplar também as explicações, justificativas e argumentações orais, uma vez que estas revelam aspectos do raciocínio que, muitas vezes, não ficam evidentes nas avaliações escritas.
BRASIL. Ministério da Educação. Secretaria de Educação Fundamental.
Parâmetros Curriculares Nacionais: atemática. Brasília, 1998 (adaptado).
Considerando as informações do texto, avalie as afirmações a seguir.
I. A observação do trabalho individual do aluno permite a análise de erros. Na aprendizagem escolar, o erro é inevitável e, muitas vezes, pode ser interpretado como um caminho para buscar o acerto.
II. Na seleção dos critérios de avaliação, é fundamental se contemplar a visão da matemática como uma construção significativa, analisando-se o progresso do estudante em relação à média de desempenho da turma.
III. Para cada conteúdo a ser desenvolvido, é importante que se reconheçam as possibilidades de conexões e que se fomente um conhecimento flexível com várias possibilidades de aplicações, valorizando o progresso do aluno.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
QUESTÃO 29
ENADE 2017: Nos Parâmetros Curriculares Nacionais (PCN) indica-se a resolução de problemas como ponto de partida da atividade matemática e discutem-se caminhos para fazer matemática na sala de aula, destacando-se, entre outras, a importância da história da matemática e das tecnologias da comunicação.
Desse modo, buscam-se estudantes mais criativos e versáteis, capazes de entender o processo como um todo, dotados de autonomia e iniciativa para resolver problemas em equipe e para utilizar diferentes tecnologias e linguagens.
BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília, 1998 (adaptado).
Considerando o trabalho em sala de aula com equações do segundo grau, escolha, entre as situações descritas nas opções a seguir, aquela na qual o professor adotou uma metodologia adequada, de acordo com a perspectiva mencionada no fragmento de texto dos PCN.
A) O professor apresentou a definição, o gráfico e, em seguida, resolveu dois exemplos, aplicando a fórmula que resolve a equação do segundo grau, utilizando a calculadora.
B) O professor explorou aspectos gráficos e algébricos com o uso de um software e, em seguida, propôs a resolução de exercícios com esse instrumento.
C) O professor expôs situações cujos modelos matemáticos resultam em equações do segundo grau e, em seguida, propôs uma pesquisa sobre a sua resolução.
D) O professor apresentou a história da fórmula que resolve a equação do segundo grau e, em seguida, utilizou a calculadora na resolução de exercícios com essa fórmula.
E) O professor propôs uma pesquisa em grupo, na internet, sobre a história da fórmula que resolve a equação do segundo grau.
QUESTÃO 30
ENADE 2017: As teorias a seguir abordam a relação entre seres humanos e máquinas e podem ser utilizadas para a compreensão da possível incorporação das tecnologias em sala de aula.
Teoria da Substituição: o ser humano é substituído pelo computador. Em sala de aula, o professor poderia ser substituído pela máquina.
Teoria da Suplementação: o computador é um suplemento do ser humano, realizando partes da resolução de um problema. Ao resolver um problema matemático, por exemplo, o aluno pode utilizar a máquina para a realização de cálculos complexos.
Teoria da Reorganização: o computador transforma qualitativamente a maneira de o ser humano pensar sobre um problema. Em sala de aula, ao resolver um problema em um ambiente informatizado, a própria maneira de o aluno refletir sobre o problema pode sofrer alterações.
TIKHOMIROV, O. K. The psychological consequences of computerization. tn 1. V. Wertsch (Org),
The concept of activity in Soviet psychology, Armonk NewYork: M. Sharpe, 1981 (adaptado).
Considerando as teorias apresentadas, avalie as afirmações a seguir.
I. Uma situação que ilustra a Teoria de Substituição é a situação em que o professor solicita aos estudantes que construam tabelas em uma planilha eletrônica com a finalidade de encontrar os zeros de uma função.
II. Uma situação que ilustra a Teoria de Suplementação é o professor solicitar aos estudantes que respondam, em seus computadores, a um questionário autocorrigível, composto por questões de múltipla escolha, disponibilizado por software destinado ao ensino de funções.
III. Uma situação que ilustra a Teoria de Reorganização é o professor solicitar aos estudantes que discutam o que ocorre no gráfico de uma função, utilizando software que permite alterar o gráfico concomitantemente à mudança dos parâmetros associados à função.
É correto o que se afirma em
A) I, apenas.
B) III, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.



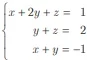
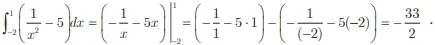






COMENTÁRIOS